
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задание № 2
|
|
Туристическая компания предлагает места в гостиницах приморского курорта. Менеджера компании интересует, насколько возрастает привлекательность гостиницы в зависимости от ее расстояния до пляжа. В таблице представлены данные по 10 гостиницам: X – расстояние от гостиницы до пляжа в километрах, Y – среднегодовой доход гостиницы, млн. руб.
Для исходных данных:
1. Найти уравнение:
(для четных вариантов) экспоненциальной регрессии 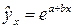 ,
,
2. Найти уравнение:
(для четных вариантов) показательной регрессии 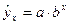 ,
,
3. Найти уравнение:
(для четных вариантов) равносторонней гиперболы 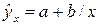 ,
,
4. Найти уравнение параболической регрессии 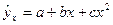 .
.
5. Найти уравнение кубической регрессии  .
.
| Вариант | Расстояние от гостиницы до пляжа в километрах (для всех вариантов) | |||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
| Среднегодовой доход гостиницы (по вариантам) | ||||||||||
| 31,2 | 27,0 | 26,1 | 26,1 | 23,1 | 23,8 | 22,3 | 21,4 | 21,8 | 22,5 |
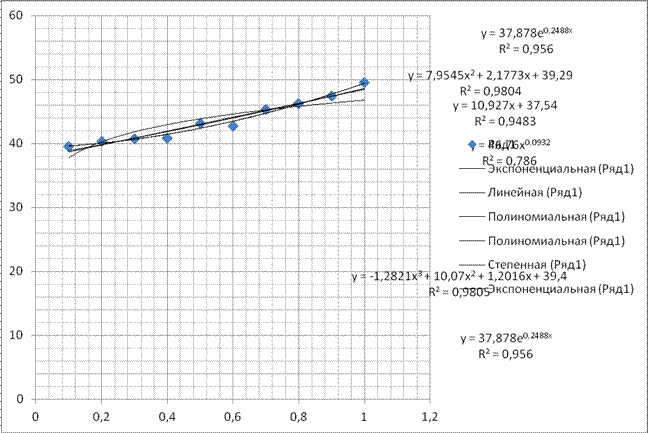
Экспоненциальная модель
Экспоненциальное уравнение регрессии имеет вид y = a ebx
Система нормальных уравнений.
a•n + b∑x = ∑y
a∑x + b∑x2 = ∑y•x
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
| x | ln(y) | x2 | ln(y)2 | x • ln(y) |
| 0.1 | 3.68 | 0.01 | 13.52 | 0.37 |
| 0.2 | 3.7 | 0.04 | 13.66 | 0.74 |
| 0.3 | 3.71 | 0.09 | 13.74 | 1.11 |
| 0.4 | 3.71 | 0.16 | 13.75 | 1.48 |
| 0.5 | 3.76 | 0.25 | 14.16 | 1.88 |
| 0.6 | 3.75 | 0.36 | 14.09 | 2.25 |
| 0.7 | 3.81 | 0.49 | 14.54 | 2.67 |
| 0.8 | 3.83 | 0.64 | 14.69 | 3.07 |
| 0.9 | 3.86 | 0.81 | 14.89 | 3.47 |
| 3.9 | 15.23 | 3.9 | ||
| 5.5 | 37.71 | 3.85 | 142.27 | 20.95 |
Для наших данных система уравнений имеет вид
10a + 5.5 b = 37.71
5.5 a + 3.85 b = 20.95
Домножим уравнение (1) системы на (-0.55), получим систему, которую решим методом алгебраического сложения.
-5.5a -3.03 b = -20.74
5.5 a + 3.85 b = 20.95
Получаем:
0.82 b = 0.21
Откуда b = 0.2488
Теперь найдем коэффициент «a» из уравнения (1):
10a + 5.5 b = 37.71
10a + 5.5 • 0.2488 = 37.71
10a = 36.34
a = 3.6344
Получаем эмпирические коэффициенты регрессии: b = 0.2488, a = 3.6344
Уравнение регрессии (эмпирическое уравнение регрессии):
y = e3.63437484e0.2488x = 37.87817e0.2488x
Показательное уравнение регрессии имеет вид y = a bx
Система нормальных уравнений.
a•n + b∑x = ∑y
a∑x + b∑x2 = ∑y•x
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
| x | ln(y) | x2 | ln(y)2 | x • ln(y) |
| 0.1 | 3.68 | 0.01 | 13.52 | 0.37 |
| 0.2 | 3.7 | 0.04 | 13.66 | 0.74 |
| 0.3 | 3.71 | 0.09 | 13.74 | 1.11 |
| 0.4 | 3.71 | 0.16 | 13.75 | 1.48 |
| 0.5 | 3.76 | 0.25 | 14.16 | 1.88 |
| 0.6 | 3.75 | 0.36 | 14.09 | 2.25 |
| 0.7 | 3.81 | 0.49 | 14.54 | 2.67 |
| 0.8 | 3.83 | 0.64 | 14.69 | 3.07 |
| 0.9 | 3.86 | 0.81 | 14.89 | 3.47 |
| 3.9 | 15.23 | 3.9 | ||
| 5.5 | 37.71 | 3.85 | 142.27 | 20.95 |
Для наших данных система уравнений имеет вид
10a + 5.5 b = 37.71
5.5 a + 3.85 b = 20.95
Домножим уравнение (1) системы на (-0.55), получим систему, которую решим методом алгебраического сложения.
-5.5a -3.03 b = -20.74
5.5 a + 3.85 b = 20.95
Получаем:
0.82 b = 0.21
Откуда b = 0.2488
Теперь найдем коэффициент «a» из уравнения (1):
10a + 5.5 b = 37.71
10a + 5.5 • 0.2488 = 37.71
10a = 36.34
a = 3.6344
Получаем эмпирические коэффициенты регрессии: b = 0.2488, a = 3.6344
Уравнение регрессии (эмпирическое уравнение регрессии):
y = e3.63437484*e0.2488x = 37.87817*1.28249x
Гиперболическое уравнение регрессии имеет вид y = b/x + a
Система нормальных уравнений.
a•n + b∑(1/x) = ∑y
a∑1/x + b∑(1/x2) = ∑y/x
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
| 1/x | y | 1/x2 | y2 | y/x |
| 39.5 | 1560.25 | |||
| 40.3 | 1624.09 | 201.5 | ||
| 3.33 | 40.7 | 11.11 | 1656.49 | 135.67 |
| 2.5 | 40.8 | 6.25 | 1664.64 | |
| 43.1 | 1857.61 | 86.2 | ||
| 1.67 | 42.7 | 2.78 | 1823.29 | 71.17 |
| 1.43 | 45.3 | 2.04 | 2052.09 | 64.71 |
| 1.25 | 46.2 | 1.56 | 2134.44 | 57.75 |
| 1.11 | 47.4 | 1.23 | 2246.76 | 52.67 |
| 49.5 | 2450.25 | 49.5 | ||
| 29.29 | 435.5 | 154.98 | 19069.91 | 1216.16 |
Для наших данных система уравнений имеет вид
10a + 29.29 b = 435.5
29.29 a + 154.98 b = 1216.16
Домножим уравнение (1) системы на (-2.93), получим систему, которую решим методом алгебраического сложения.
-29.29a -85.82 b = -1276.02
29.29 a + 154.98 b = 1216.16
Получаем:
69.16 b = -59.85
Откуда b = -0.8585
Теперь найдем коэффициент «a» из уравнения (1):
10a + 29.29 b = 435.5
10a + 29.29 • (-0.8585) = 435.5
10a = 460.65
a = 46.0647
Получаем эмпирические коэффициенты регрессии: b = -0.8585, a = 46.0647
Уравнение регрессии (эмпирическое уравнение регрессии):
y = -0.8585 / x + 46.0647
Уравнение параболической регрессии имеет вид y = a2x2 + a1x + a0
Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a0n + a1∑x + a2∑x2 = ∑y
a0∑x + a1∑x2 + a2∑x3 = ∑yx
a0∑x2 + a1∑x3 + a2∑x4 = ∑yx2
| x | y | x2 | y2 | x y | x3 | x4 | x2 y |
| 0.1 | 39.5 | 0.01 | 1560.25 | 3.95 | 0.001 | 0.0001 | 0.4 |
| 0.2 | 40.3 | 0.04 | 1624.09 | 8.06 | 0.008 | 0.0016 | 1.61 |
| 0.3 | 40.7 | 0.09 | 1656.49 | 12.21 | 0.027 | 0.0081 | 3.66 |
| 0.4 | 40.8 | 0.16 | 1664.64 | 16.32 | 0.064 | 0.0256 | 6.53 |
| 0.5 | 43.1 | 0.25 | 1857.61 | 21.55 | 0.13 | 0.0625 | 10.78 |
| 0.6 | 42.7 | 0.36 | 1823.29 | 25.62 | 0.22 | 0.13 | 15.37 |
| 0.7 | 45.3 | 0.49 | 2052.09 | 31.71 | 0.34 | 0.24 | 22.2 |
| 0.8 | 46.2 | 0.64 | 2134.44 | 36.96 | 0.51 | 0.41 | 29.57 |
| 0.9 | 47.4 | 0.81 | 2246.76 | 42.66 | 0.73 | 0.66 | 38.39 |
| 49.5 | 2450.25 | 49.5 | 49.5 | ||||
| 5.5 | 435.5 | 3.85 | 19069.91 | 248.54 | 3.03 | 2.53 |
Для наших данных система уравнений имеет вид
10a0 + 5.5a1 + 3.85a2 = 435.5
5.5a0 + 3.85a1 + 3.03a2 = 248.54
3.85a0 + 3.03a1 + 2.53a2 = 178
Получаем a2 = 7.955, a1 = 2.177, a0 = 39.29
Уравнение регрессии:
y = 7.955x2+2.177x+39.29
Уравнение кубической регрессии:
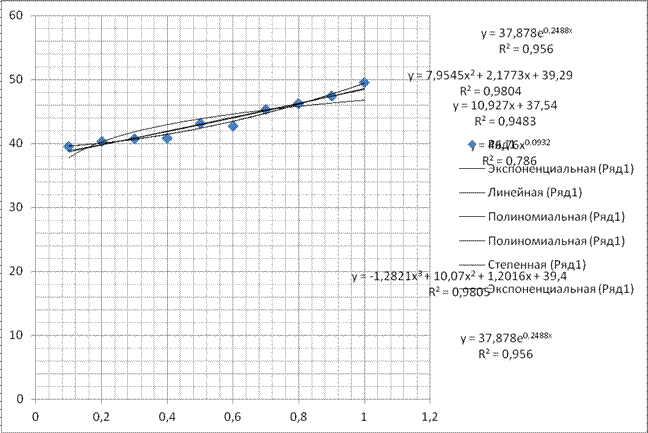
y = -1,2821 x3+10,07x2+1,2016x+39.4
Уравнение кубической регрессии является наилучшим, так как коэффициент детерминации самый большой 0,9805
Date: 2015-09-22; view: 1577; Нарушение авторских прав