Уравнение Эйлера для работы лопастного колеса

Для определения суммарного момента реакции лопаток рабочего колеса при взаимодействии их с потоком жидкости воспользуемся теоремой об изменении момента количества движения. Согласно этой теореме при установившемся движении изменение момента количества движения потока жидкости, проходящее через рабочее колесо нагнетателя в единицу времени, равно моменту сил реакции лопаток.

Применяя данную теорему к движению жидкости через рабочее колесо нагнетателя, допустим, что это движение установившееся, струйное, без гидравлических потерь. Рассмотрим изменение момента количества движения, массы жидкости за 1с. При этом масса участвующей в движении жидкости можно определить по следующей зависимости:

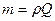(2.15)

где, – плотность жидкости;

Q – подача нагнетателя.

Момент количества движения относительно оси рабочего колеса во входном сечении при скорости движения в этом сечении C₁ (рисунок 2.3), можно определить по следующей зависимости:

M₁= Qc₁r₁

А момент количества движения на выходе из рабочего колеса – по следующей зависимости:

M₂= Qc₂r₂

где,

r₁ и r₂ - расстояния от оси колеса до вектора входной и выходной скоростей.

Сумма моментов сил, действующих на лопатку рабочего колеса нагнетателя спроецированных на радиус определяют по следующей зависимости:

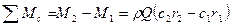
Так как

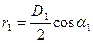, а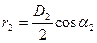

то

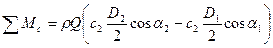(2.16)

С другой стороны на массу жидкости, заполняющей межлопастные каналы рабочего колеса, действуют 4 группы внешних сил: сила тяжести, силы давления в сечениях (входа-выхода), динамические силы (центробежные силы) со стороны рабочего колеса и силы трения жидкости на обтекаемых поверхностях

где, М_G – момент силы тяжести;

М_P – момент сил давления;

М_F – момент сил трения;

М_К – момент от динамических сил.

Момент силы тяжести всегда равен 0, так как плечо этих сил равно 0 (они проходят через ось вращения колеса). Момент сил давления в расчетных сечениях по той же причине равен 0. А поскольку силами трения пренебрегают, то момент сил трения тоже равен 0. Следовательно, момент всех внешних сил относительно оси вращения колеса сводится к моменту динамического взаимодействия рабочего колеса на протекающую через него жидкость, т.е.

(2.17)

Известно, что мощность, передаваемая жидкости рабочим колесом, т.е. произведение 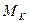на окружную скорость w₀ равна произведению расхода Q на теоретическое давление P _т, создаваемое нагнетателем.

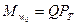_, (2.18)

Следовательно, уравнение (2.16) с учетом выражений (2.17) и (2.18) будет иметь вид

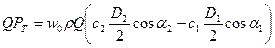(2.19)

Известно, что окружные скорости u₁ и u₂ можно представить в виде:

(2.20)

из этого следует

_;

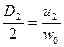
Подставив выражения в (2.19) и (2.20) и разделив его на Q, получим

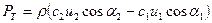(2.21)

или с учетом того, что 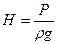или P= gH, уравнение (2.21) примет вид:

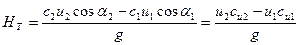(2.22)

Зависимость (2.22) называют основным уравнением лопастных нагнетателей или уравнением Эйлера.

Уравнения (2.21) и (2.22) выведены из условия пренебрежения силами трения и учетом того, что рабочее колесо имеет бесконечное число тонких лопаток (z= ).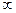

Известно, что в рабочее колеса большинства центробежных нагнетателей жидкость поступает радиально (a=90⁰, следовательно, с₁=0) поэтому уравнение (2.21) и (2.22) можно записать в виде:

(2.23)

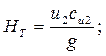(2.24)

Для осевых нагнетателей в силу того, что переносные (окружные) скорости на входе и выходе одинаковы уравнение (2.22) имеет вид:

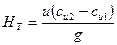(2.25)

Основное уравнение лопастного нагнетателя показывает, что теоретическое давление и напор, тем больше, чем больше окружная скорость на внешней окружности рабочего колеса u=pD₂n, т.е. чем больше его диаметр, частота вращения и угол b₂.

2.4 Влияние угла (β₂) выхода потока на напор нагнетателя

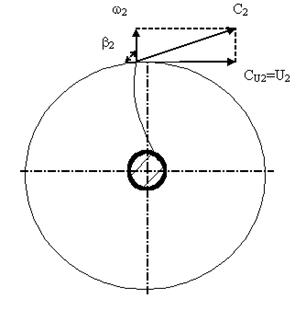
Угол выхода потока b₂ зависит от формы лопаток. Существуют три вида лопаток: загнутые (по ходу вращения) назад; с радиальным выходом; загнутые вперед.

а) б)

в)

Рис. 2.5. Зависимость угла выходы от формы лопаток.

При равных геометрических размерах колес и постоянном значении u₂ c возрастанием b₂ увеличивается окружная составляющая абсолютной скорости с_w. Следовательно, с увеличением b₂ напор насоса увеличивается и у рабочего колеса с лопатками, загнутыми вперед, он будет наибольшим. Однако в практике насосостроения чаще используют рабочие колеса с лопатками, загнутыми назад. Это объясняется следующими причинами:

1. Основным назначением нагнетателей является создание статистического напора, а колеса с лопатками загнутыми вперед обладают малым коэффициентом статического напора (k_с<0,5). У рабочих колес с радиальными лопатками k_с=0,5, а с лопатками, загнутыми назад, (k_с>0,5), (k= )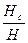

Основное увеличение напора у них происходит за счет возрастания динамической составляющей скорости (с₂).

2. Лопатки, загнутые назад, с гидродинамической точки зрения более удобообтекаемые при переменном режиме работы нагнетателей, диапазон скоростей безотрывного обтекания значительно шире. Следовательно, гидравлические потери при движении жидкой среды по каналам будут меньше, а КПД насоса выше. Обычно принимают следующие значения углов входа и выхода для лопаток, загнутых назад:

b₁=14-25 ⁰

b₂=15-40 ⁰

Действительное давление и напор, развиваемый нагнетателем, меньше теоретических. Давление, развиваемое нагнетателем, уменьшается главным образом из-за того, что при конечном числе лопастей рабочего колеса не все частицы жидкости отклоняются равномерно, вследствие чего уменьшается абсолютная скорость (с₂). Влияние конечного числа лопастей учитывается введением поправочного коэффициента К,

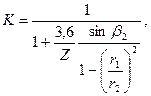(2.26)

где

Z – число лопастей рабочего колеса нагнетателя.

Кроме того, часть энергии расходуется на преодоление гидравлических сопротивлений, которые учитываются гидравлическим КПД.

(2.27)

С учетом этих поправок полное давление определяют следующим выражением:

(2.28)

А полный напор:

(2.29)

Угол a₂ принимают обычно в пределах 8-14 ⁰.

Полное давление (напор) можно выразить в виде зависимости от абсолютной, переносной и относительной скоростей потока. Для этого еще раз воспользуемся треугольником скоростей (см. рис.2.4)

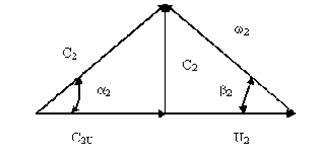
Согласно теореме косинусов имеем:

(2.30)

и подставив в уравнение (2.69), вместо значения

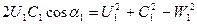
получим

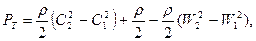(2.31)

Из уравнения видно, что давление, создаваемое нагнетателем, складывается из прироста кинетической энергии абсолютного движения, повышения статического давления от работы центробежных сил и преобразования кинетической энергии относительного движения в межлопасных каналах.

Отношение скорости закручивания к окружной скорости называется коэффициентом закручиванияj.

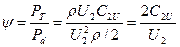
Date: 2015-09-24; view: 2047; Нарушение авторских прав