Теория Е.Е.Жуковского о подъемной силе элемента лопатки

Для определения сил взаимодействия лопасти нагнета­теля с обтекающей ее жидкостью Н. Е. Жуковский при­менил теорему импульсов к контрольной поверхности в виде круглого цилиндра.

Повторим вкратце вывод теоремы Н. Е. Жуковско­го для случая, когда длина образующей цилиндра рав­на b, радиус площади основания r, а его ось совпадает с осью аэродинамического профиля (см. рис. 2.2).

Запишем уравнение, выражающее теорему импульсов в проекции на координатные оси х и у. Для этого выберем на контрольной поверхности элементарную пло­щадку ds = bdl. На этой площадке действуют только силы гидродинамического давления, равные pds. Со­ставляющие скорости потока жидкости, проходящего через контрольную поверхность в продольном и попереч­ном направлении, обозначим через u и 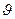соответственно. Проекция на ось х всех сил, действующих на массу жидкости, заключенную внутри контрольной поверхно­сти, равна

— F_x — ; (2.1)

на ось у —

F_y — ; (2.2)

Действие этих сил приводит к изменению количества движения ( Qw) массы жидкости, проходящей в едини­цу времени через контрольную поверхность. Проекция на ось х изменения количества движения массы жидко­сти, прошедшей в единицу времени через поверхность s, равна:

(2.3)

на ось у —

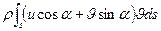(2.4)

Выражение (u cos 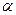+ 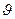sin 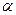) ds определяет расход жидкости, проходящий через элементарное живое сече­ние ds на контрольной поверхности.

Используя выражения (2.1) и (2.3), уравнение сохра­нения импульса в проекции на ось х запишем в виде

— F_х — 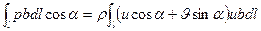(2.5)

Воспользуемся известным соотношением

dl — rd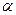

и подставим его в уравнение (2.5). Учитывая, что b = const, заменяя переменные и пределы интегрирования, вместо выражения (2.5) получаем

— F_x — 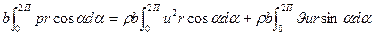(2.6)

При увеличении радиуса окружности цилиндриче­ский поверхности до некоторого конечного значения r=r₀, при котором поток, проходящий через контроль­ную поверхность, становится невозмущенным (от воз­действия профиля), видно, что продольная составляю­щая скорости и стремится к скорости невозмущенного потока w₀) поперечная составляющая скорости 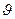стре­мится к нулю, а давление р на контрольной поверхно­сти стремится к давлению в невозмущенном потоке р₀. С учетом сказанного уравнение (2.6) перепишется в виде

— F_x — p₀ r₀ b 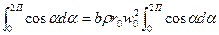(2.7)

Имея в виду, что определенный интеграл

,

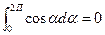из выражения (2.7) получаем

F_x=0. (2.8)

Полученное выражение (2.8) показывает, что в слу­чае обтекания тела потоком идеальной жидкости сила лобового сопротивления отсутствует. Поэтому для воз­никновения лобового сопротивления необходимо нали­чие в потоке вязких сил.

Запишем уравнение сохранения импульса в проек­ции на ось у, для чего воспользуемся выражениями (2.2) и (2.4). В этом случае имеем

F_y — 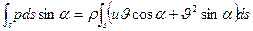(2.9)

Преобразуем правую часть уравнения (2.9), подста­вив в него выражение, полученное из треугольника ско­ростей (см. рис. 2.3):

.

Имеем последовательно

=

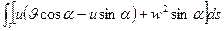
Заметим, что выражение

есть проекция скорости потока w на касательную к кон­трольной поверхности, выраженная через составляющие и и . Тогда с учетом принятых обозначений уравнение (2.9) можно записать в виде

F_y — b (2.10)

Увеличивая радиус окружности цилиндрической по­верхности до некоторого конечного значения r₀, видим, что в невозмущенном потоке продольная составляющая скорости и в первом слагаемом правой части стремится к w₀, скорость потока w во втором слагаемом правой части также стремится к w₀. Имея в виду сказанное выше, а также то, что определенный интеграл

,

уравнение (1.10) можно представить в виде

F_y = . (2.11)

Сравнивая интеграл правой части выражения (2.11) с равенством (2.15), видим, что подъемная сила F_y про­порциональна циркуляции скорости Г по замкнутому контуру. Таким образом, для подъемной силы, возни­кающей на профиле длиной b, получаем формулу Н. Е. Жуковского:

F_y = . (2.12)

Из теоремы Н. Е. Жуковского следует, что если при обтекании аэродинамического профиля потенциальным потоком жидкости имеет место циркуляция скорости во­круг профиля, то возникает подъемная сила, направлен­ная по нормали к вектору относительной скорости.

Date: 2015-09-24; view: 624; Нарушение авторских прав