
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Зв’язок між напруженістю електростатичного поля та потенціалом
|
|
Ми вже переконалися, що електричне поле можна характеризувати як вектором напруженості електричного поля, так і потенціалом. Хоч одна із величин векторна, а друга скалярна, вони характеризують той самий об’єкт. Отже, можна очікувати, що між ними існує зв’язок.
 Нехай є електричне поле
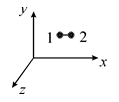
Нехай є електричне поле  . Виберемо декартову систему координат. Електричне поле має три проекції вздовж осей
. Виберемо декартову систему координат. Електричне поле має три проекції вздовж осей 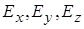 . Виберемо 2 точки із координатами
. Виберемо 2 точки із координатами 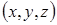 та
та 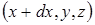 . Ці точки лежать на прямій, паралельній осі
. Ці точки лежать на прямій, паралельній осі  , на нескінченно малій відстані
, на нескінченно малій відстані  .
.
Різницю потенціалів між точками 1 і 2 можна записати двома способами. З одного боку,
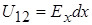 ,
,
оскільки вздовж напрямку  діє лише одна складова вектора напруженості електричного поля. З іншого боку,
діє лише одна складова вектора напруженості електричного поля. З іншого боку,
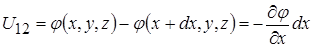 ,
,
скористалися малим приростом потенціалу по осі  . По решті координат приросту немає, отже складові відсутні.
. По решті координат приросту немає, отже складові відсутні.
Порівнявши обидва рівняння, маємо
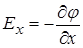 .
.
Оскільки вісь  вибиралася нами довільно, а всі компоненти рівноцінні, то ніхто не заборонить нам записати такі ж рівняння і для інших координат
вибиралася нами довільно, а всі компоненти рівноцінні, то ніхто не заборонить нам записати такі ж рівняння і для інших координат
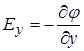 ;
; 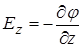 .
.
Знов згадаємо, що напруженість електричного поля – вектор, тому
 .
.
Підставивши вирази для координат вектору напруженості електричного поля через потенціали, маємо
 .
.
Оскільки потенціал є скаляром, винесемо його з під знаку вектора
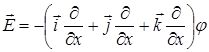 .
.
Остаточно, отримуємо зв’язок між вектором напруженості електричного поля та потенціалом
 .
.
Цей зв’язок дає нам можливість ввести одиниці виміру напруженості електричного поля, яку ми так тактовно обминули раніше. В системі Гаусса вона не має власної назви, тому не буду вас плутати одиницями CGSE.
В системі СІ напруженість електричного поля вимірюється
 .
.
Дуже широко вживається і 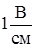 , це похідна одиниця системи СІ, не системи Гаусса, оскільки у ній немає В.
, це похідна одиниця системи СІ, не системи Гаусса, оскільки у ній немає В.
Date: 2015-09-24; view: 460; Нарушение авторских прав