Транспортная задача линейного программирования в сетевой постановке

В ТЗЛП в сетевой постановке учитываются реальные транспорт­ные связи между поставщиками и потребителями, поэтому в ре­зультате ее решения получается не просто оптимальный план перевозок, но и план распределения транспортных потоков по дугам транспортной сети. Очевидно, что максимальные по мощности транспортные потоки должны проходить по дугам, имеющим ми­нимальную оценку, то есть по наиболее коротким и дешевым транспортным коммуникациям

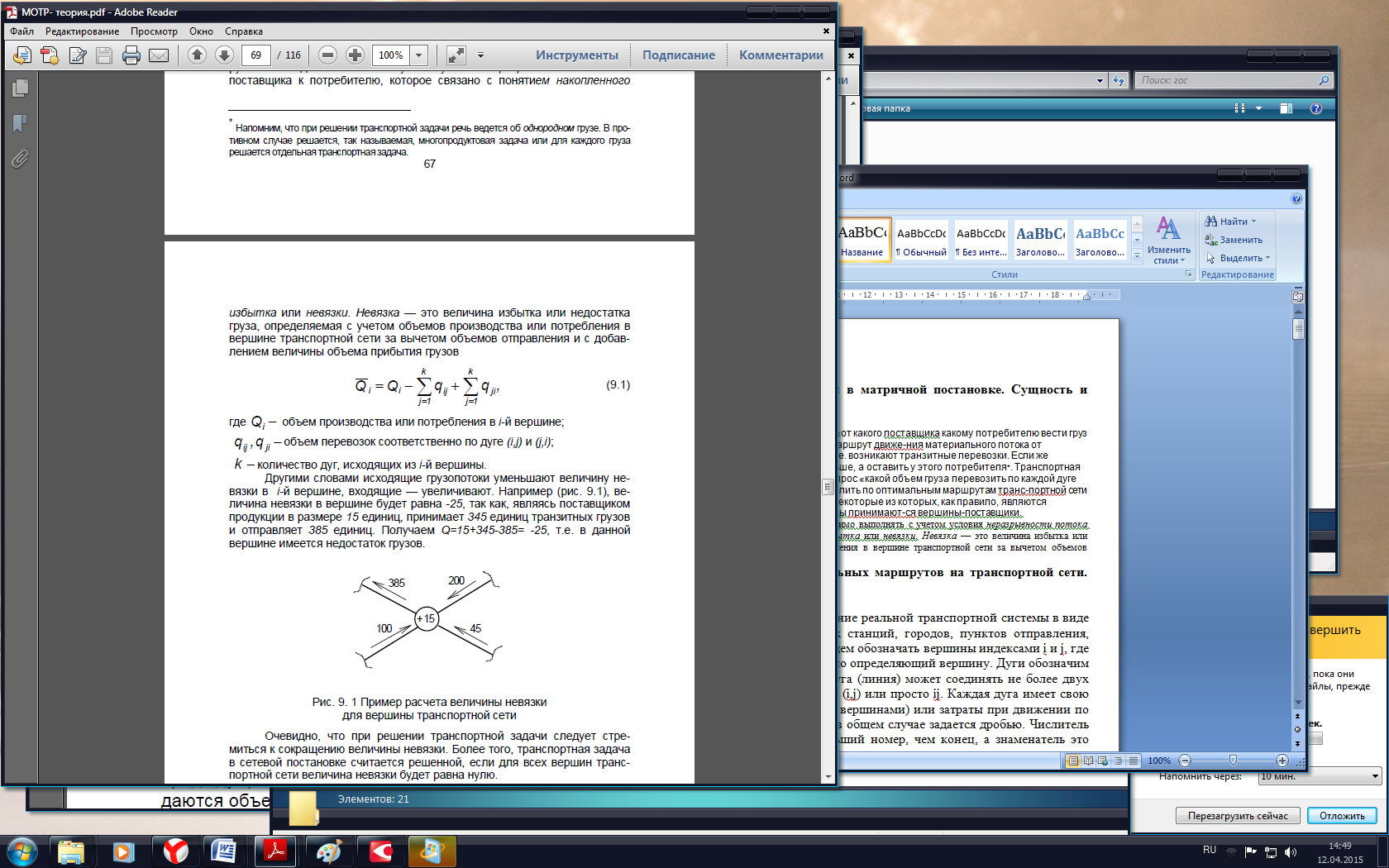
Невязка — это величина избытка или недостатка груза, определяемая с учетом объемов производства или потребления в вершине транспортной сети за вычетом объемов отправления и с добав­лением величины объема прибытия грузов. 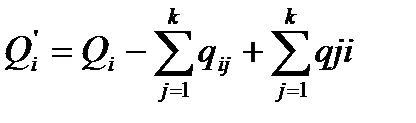Другими словами исходящие грузопотоки уменьшают величину не­вязки в i-й вершине, входящие — увеличивают. Например, ве­личина невязки в вершине будет равна -25, так как, являясь поставщиком продукции в размере 15 единиц, принима

ет 345 единиц транзитных грузов и отпр-ет 385 единиц. Получаем Q=15+345-385= -25, т.е. в данной вершине им. недостаток грузов.

Алгоритм решения ТЗЛП в сетевой постановке методом сокраще­ния невязки состоит из следующих действий:

1) построить таблицу оптимальных путей для заданной транс­портной сети. В качестве начальных вершин принимаются все вершины-поставщики

2) по найденным маршрутам транспортной сети распределить транспортные потоки так, чтобы полностью удовлетворить спрос всех вершин-потребителей. После этого объемы спроса в вершинах-потребителях должны быть равны нулю, а объем производства в вершине-поставщике может остаться поло­жительным, стать нулевым или отрицательным. То есть по­ставщик может превратиться в потребителя;

3) скорректировать систему оценок дуг транспортной сети, за­груженных перевозками. Для этого делается отрицательной оценка дуги, направленной навстречу транспортному потоку. В результате, при следующей итерации, оптимальными бу­дут маршруты, включающие в себя дуги с минимальной (от­рицательной) оценкой, то есть пути, встречные найденным маршрутам. Встречные транспортные потоки взаимопога­шаются. Для этого из большего по мощности трансп. потока вычитается мощность более слабого потока;

4) повторять предыдущие действия до тех пор, пока величина невязки плана перевозок не станет нулевой, то есть когда все объемы производства и потребления не компенсируются транспортными потоками.

Транспортная задача линейного программирования отвечает на вопрос «от какого поставщика какому потребителю вести груз и в каком объеме?» без учета структуры реальной транспортной сети. Маршрут движения материального потока от поставщика к потребителю может проходить через другого поставщика, т.е. возникают транзитные перевозки. Если же транзитная вершина является потребителем, то груз можно не везти дальше, а оставить у этого потребителя. Транспортная задача в сетевой постановке позволяет дополнительно дать ответ на вопрос «какой объем груза перевозить по каждой дуге транспортной сети?». Для этого объемы перевозок необходимо распределить по оптимальным маршрутам транспортной сети от начальной вершины (поставщика) до вершин, образующих маршрут, некоторые из которых, как правило, являются потребителями. При этом строится ТОП, в которой за начальные вершины принимаются вершины-поставщики.

Дальнейшее распределение грузопотоков по оптимальным маршрутам необходимо выполнять с учетом условия неразрывности потока от поставщика к потребителю, которое связано с поняти ем накопленного избытка или невязки.

Невязка — это величина избытка или недостатка груза, определяемая с учетом объемов производства или потребления в вершине транспортной сети за вычетом объемов отправления и с добавлением величины объема прибытия грузов

Очевидно, что при решении транспортной задачи следует стремиться к сокращению величины невязки. Более того, транспортная задача в сетевой постановке считается решенной, если для всех вершин транспортной сети величина невязки будет равна нулю.

В процессе распределения перевозок по оптимальным маршрутам от поставщиков к потребителям часто возникают встречные перевозки. Так как мы в задаче имеем дело с однородным грузом, то необходимо их взаимопоглащать. Для этого из большего объема перевозки вычитается меньший, разница будет составлять окончательный объем перевозок по дуге, а направление этой перевозки будет совпадать с направлением перевозки с первоначальным большим объемом.

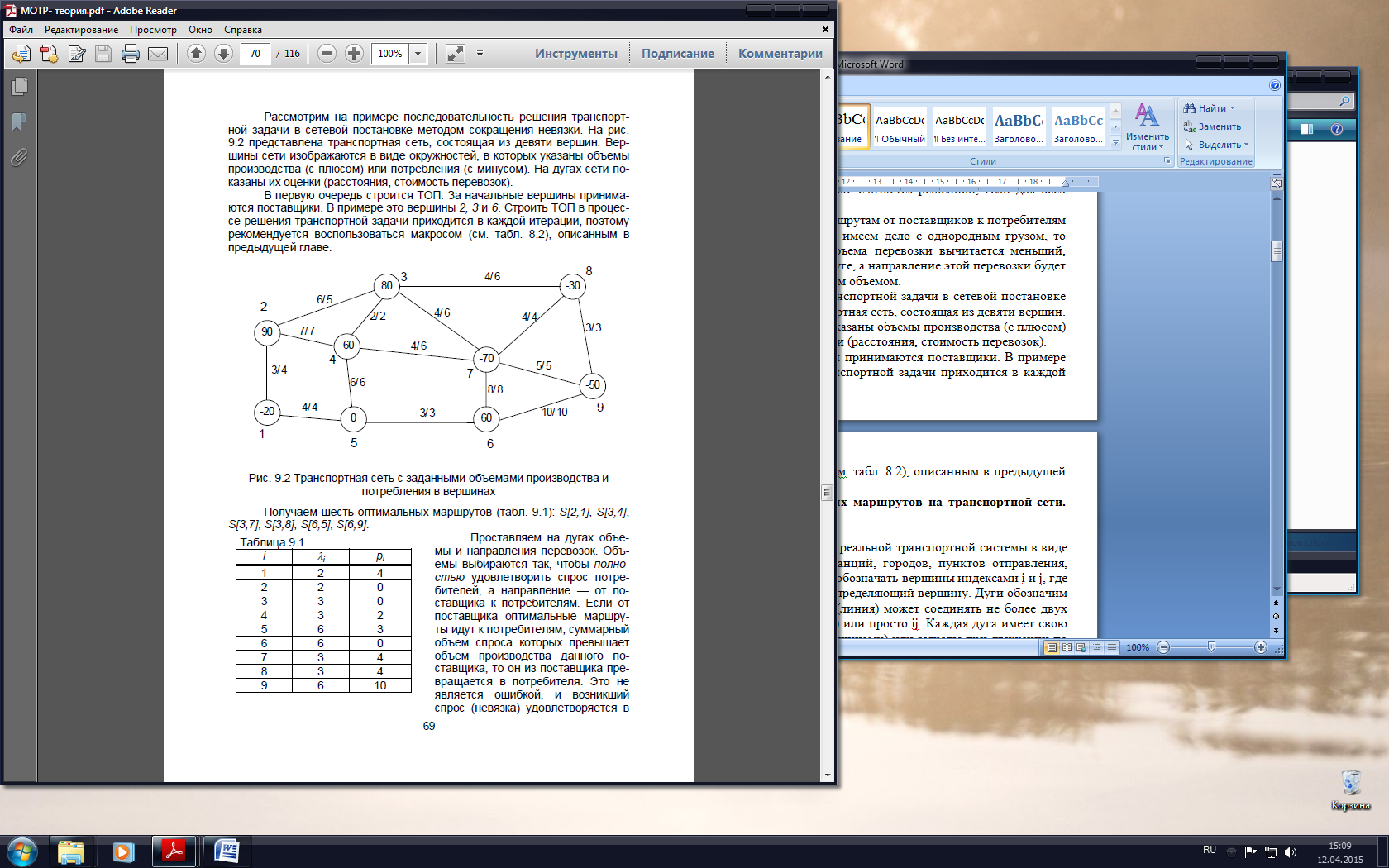
Рассмотрим на примере последовательность решения транспортной задачи в сетевой постановке методом сокращения невязки. На рис. 9.2 представлена транспортная сеть, состоящая из девяти вершин. Вершины сети изображаются в виде окружностей, в которых указаны объемы производства (с плюсом) или потребления (с минусом). На дугах сети показаны их оценки (расстояния, стоимость перевозок).

В первую очередь строится ТОП. За начальные вершины принимаются поставщики. В примере это вершины 2, 3 и 6. Строить ТОП в процессе решения транспортной задачи приходится в каждой итерации, поэтому рекомендуется воспользоваться макросом (см. табл. 8.2), описанным в предыдущей главе.

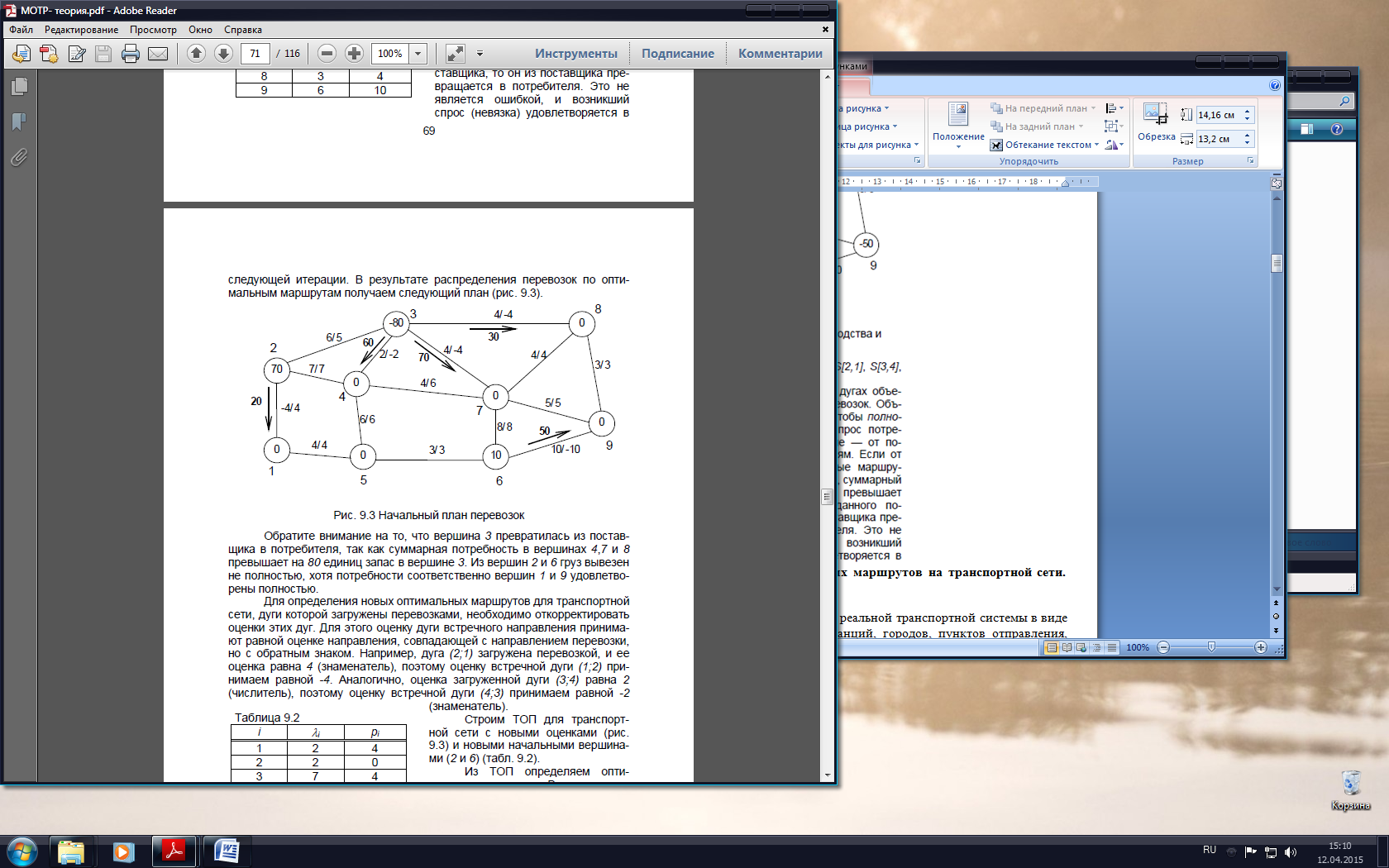
Обратите внимание на то, что вершина 3 превратилась из поставщика в потребителя, так как суммарная потребность в вершинах 4, 7 и 8 превышает на 80 единиц запас в вершине 3. Из вершин 2 и 6 груз вывезен не полностью, хотя потребности соответственно вершин 1 и 9 удовлетворены полностью.

Для определения новых оптимальных маршрутов для транспортной сети, дуги которой загружены перевозками, необходимо откорректировать оценки этих дуг. Для этого оценку дуги встречного направления принимают равной оценке направления, совпадающей с направлением перевозки, но с обратным знаком. Например, дуга (2;1) загружена перевозкой, и ее оценка равна 4 (знаменатель), поэтому оценку встречной дуги (1;2) принимаем равной -4. Аналогично, оценка загруженной дуги (3;4) равна 2 (числитель), поэтому оценку встречной дуги (4;3) принимаем равной -2 (знаменатель).

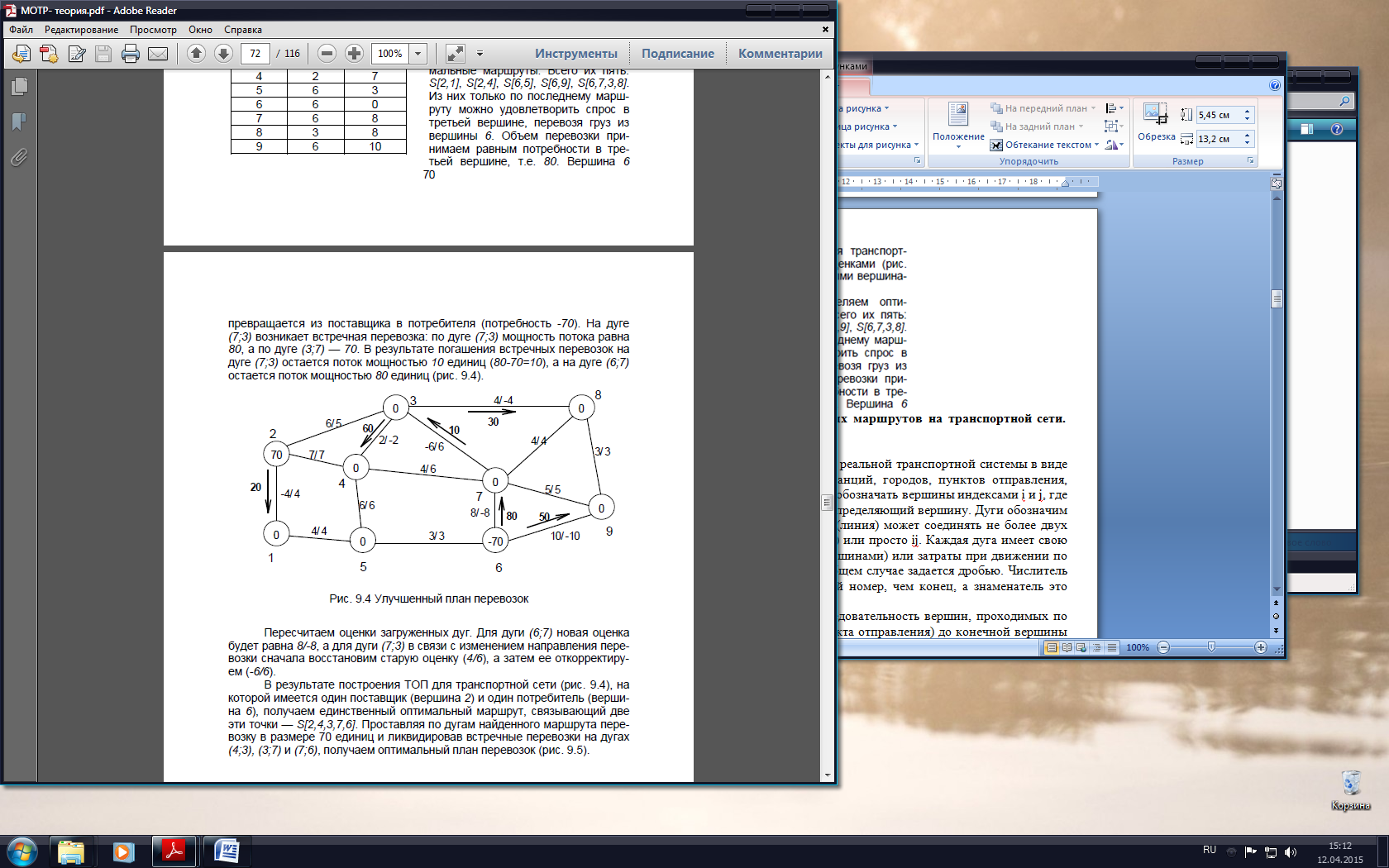
Пересчитаем оценки загруженных дуг. Для дуги (6;7) новая оценка будет равна 8/-8, а для дуги (7;3) в связи с изменением направления перевозки сначала восстановим старую оценку (4/6), а затем ее откорректируем (-6/6).

В результате построения ТОП для транспортной сети (рис. 9.4), на которой имеется один поставщик (вершина 2) и один потребитель (вершина 6), получаем единственный оптимальный маршрут, связывающий две эти точки — S[2,4,3,7,6]. Проставляя по дугам найденного маршрута перевозку в размере 70 единиц и ликвидировав встречные перевозки на дугах (4;3), (3;7) и (7;6), получаем оптимальный план перевозок (рис. 9.5).

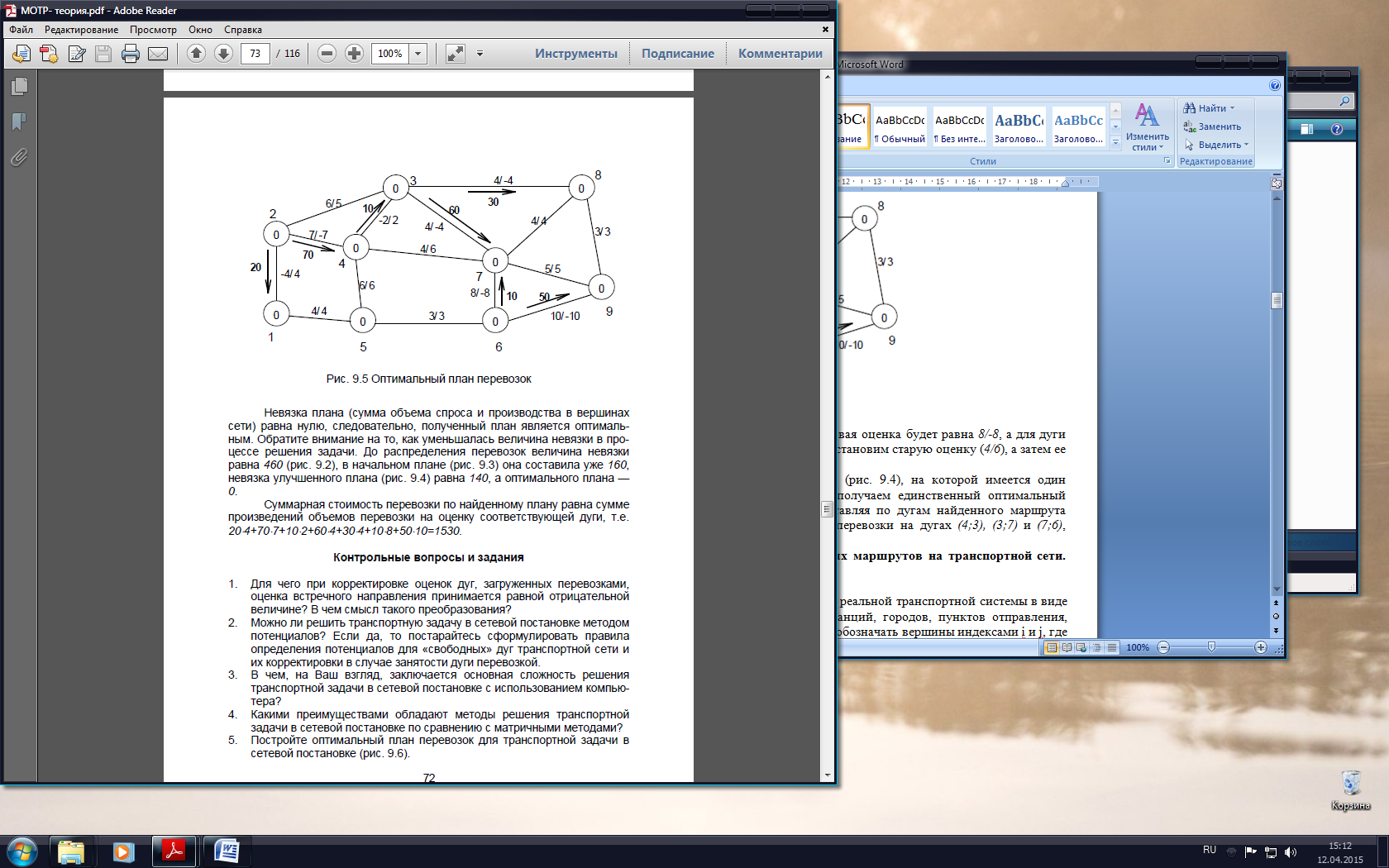
Невязка плана (сумма объема спроса и производства в вершинах сети) равна нулю, следовательно, полученный план является оптимальным. Обратите внимание на то, как уменьшалась величина невязки в процессе решения задачи. До распределения перевозок величина невязки равна 460 (рис. 9.2), в начальном плане (рис. 9.3) она составила уже 160, невязка улучшенного плана (рис. 9.4) равна 140, а оптимального плана — 0.

Суммарная стоимость перевозки по найденному плану равна сумме произведений объемов перевозки на оценку соответствующей дуги, т.е. 20 ⋅ 4+70 ⋅ 7+10 ⋅ 2+60 ⋅ 4+30 ⋅ 4+10 ⋅ 8+50 ⋅ 10=1530.

Date: 2015-09-24; view: 2520; Нарушение авторских прав