
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Расчет ригеля на выносливость
|
|
Расчет на выносливость производится по нагрузкам первого случая по условию:
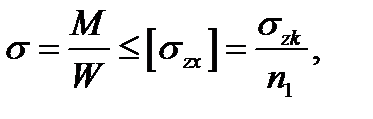 (4.15)
(4.15)
где σzk - предел выносливости с учетом коэффициента асимметрии цикла z, эффективного коэффициента концентрации k, размеров детали и ее термообработки; n1 - коэффициент запаса прочности при нагрузках первого случая.
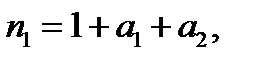 (4.16)
(4.16)
где a1 - коэффициент, учитывающий минимальный запас прочности, a1 = 0.3;
а2 - коэффициент, учитывающий неоднородность материала, а2 = 0.1.

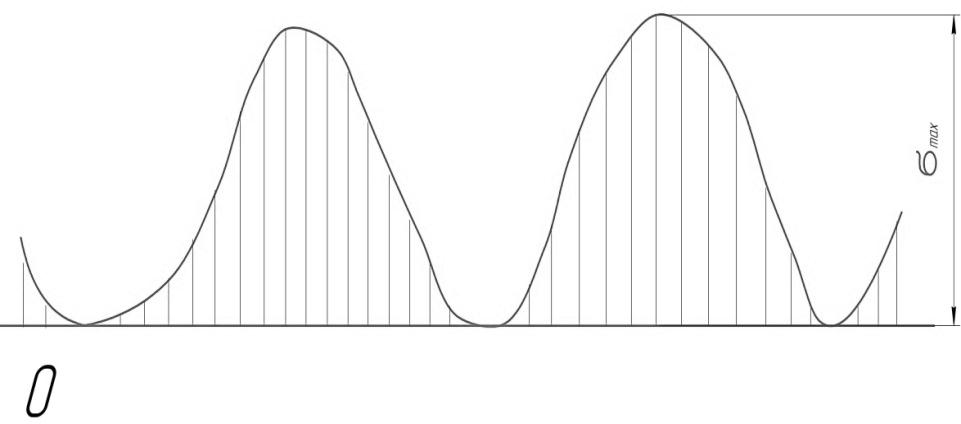
Рисунок 4.5 График для пульсирующего цикла напряжения растяжения.
Для пульсирующего цикла напряжения растяжения (рисунок 4.5) при z = 0:
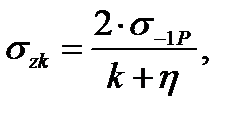 (4.17)
(4.17)
где k - эффективный коэффициент концентраций напряжений, k = 2;
η - коэффициент чувствительности материала к асимметрии цикла, для СтЗ,
η = 0.2
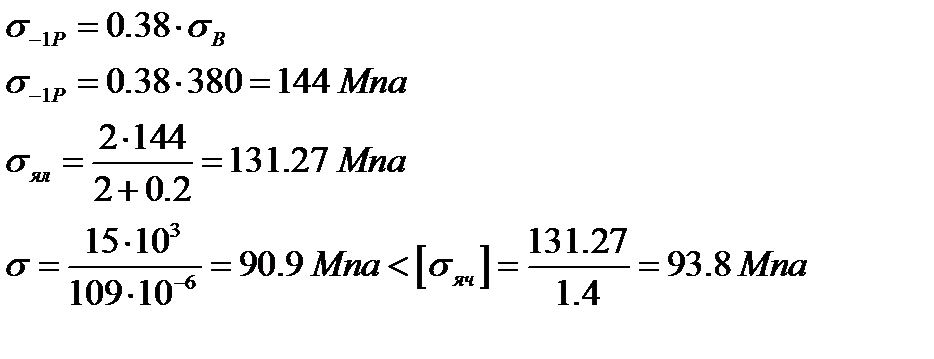
Т.е. условие выполняется.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| КП 00 00 00 05 ПЗ |
| Разраб. |
| Куцко |
| Провер. |
| Новосельская |
| Реценз. |
| Н. Контр. |
| Утверд. |
| Новосельская |
| Расчет стоек рамы на прочность и определение профиля их сечения |
| Лит. |
| Листов |
| БГТУ 4 17 08 17 13 |
Расчет статически неопределимой рамы от внешних сил заключается в определении реакций опор и максимального изгибающего момента в опасных сечениях. Расчет производим согласно методике изложенной в [4].
Для расчета необходимо определить нагрузки, действующие на раму с учетом собственного веса рамы.
Вес балки:
 (5.1)
(5.1)
где 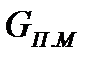 – масса 1 погонного метра балки,
– масса 1 погонного метра балки, 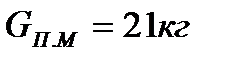 ;
;
l – длина балки, м.
Тогда общий вес балок составит:
Предварительно по ГОСТ 8239-89 выбираем профиль стоек в виде двутавра №20 [5]: Jx = 1840 см4, Jy = 115 см4, Wx = 184 см3, Wy = 23.1 см3, ix = 8.28 см, iУ = 2.07 см, Sx = 104 см3, h = 200 мм, b = 100 мм, d = 5.2 мм, t = 8.4 мм, R = 9.5 мм,r=4 мм, A = 26.8 см2 , Gп.м. = 21 кг.
Вес стоек будет равен:
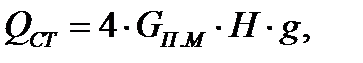 (5.2)
(5.2)
где Н – высота стоек равная 2.2 м.
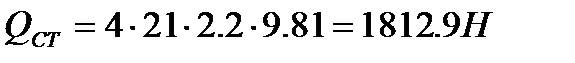
Общая нагрузка, действующая на 4 опоры фундамента, будет равна:
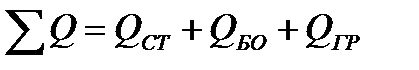 (5.3)
(5.3)
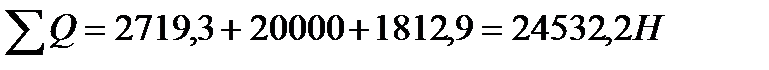
На одну опору будет действовать следующая нагрузка:
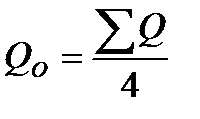 (5.4)
(5.4)
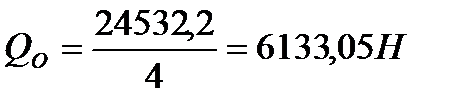
Рассматриваемая рама (рисунок 5.1) представляет симметричную (геометрическую и упругую) систему (рисунок 5.2), т.к. ее геометрическая схема имеет ось симметрии. Жесткость (EJ1) симметрично расположенных элементов одинакова. В этом случае целесообразно основную систему гак же выбрать симметричной, разрезав раму по оси ее симметрии на две части. За лишние неизвестные принимаем внутренние усилия: продольную силу х1, поперечную силу х2 и изгибающий момент х3 в сечении.

Рисунок 5.1 - Статически неопределимая рама.

Рисунок 5.2 - Симметричная рама.
Эпюры моментов (М1 и М3) от симметричных единичных усилий х1 и х3 симметричны относительно оси разреза, а эпюра (М2) от кососимметричного единичного усилия х2 кососимметрична (рисунок 5.3).
Очевидно, что по правилу Верещагина результат перемножения симметричной эпюры на кососимметричную равен нулю. Отсюда следует, что побочные перемещения δ12= δ21=0 и δ23= δ32=0. Канонические уравнения имеют вид:
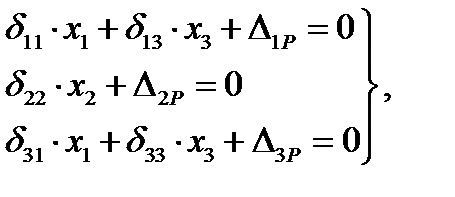 (5.5)
(5.5)
где - х1, х2,x3 - неизвестные изгибающие моменты;
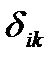 - перемещение по i-ому направлению от единичного силового фактора, заменяющего хk;
- перемещение по i-ому направлению от единичного силового фактора, заменяющего хk;
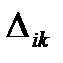 - это перемещение по i-ому направлению от заданных нагрузок.
- это перемещение по i-ому направлению от заданных нагрузок.
Таким образом, система трех уравнений с тремя неизвестными разбилась на следующие уравнения с двумя симметричными неизвестными х1 и х3 и одно уравнение с одной кососимметричной неизвестной х2, что значительно сокращает объем вычислений по определению лишних неизвестных. Все коэффициенты при неизвестных вычисляем по правилу Верещагина.

Рисунок 5.3 - Эквивалентная система с заданными нагрузками и приложенными единичными силами.
Для определения коэффициентов, входящих в систему, построим единичные (рисунок 5.4) и грузовую (рисунок 5.5), (от заданных нагрузок) эпюры изгибающих моментов.
Эпюры изгибающих моментов от единичных сил:



Рисунок 5.3 - Эпюра моментов от единичных сил.
Грузовая эпюра от заданных нагрузок:

Рисунок 5.5 - Эпюра моментов от заданных нагрузок.
Главные перемещения:
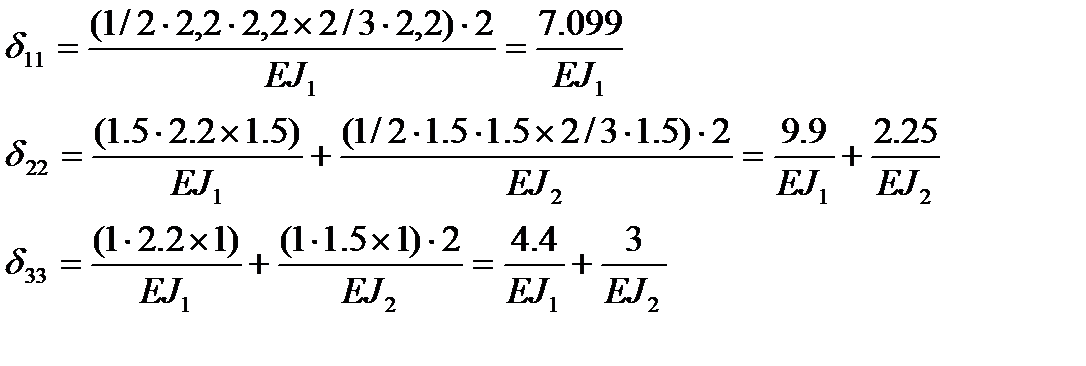
Побочные перемещения:
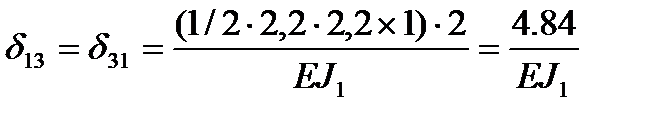
Грузовые перемещения (перемещения от заданной нагрузки):
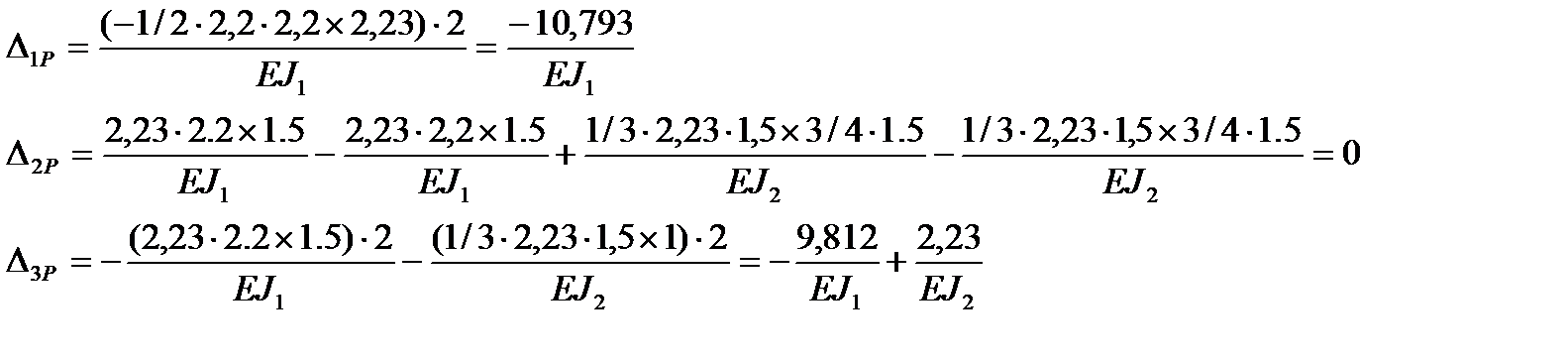
Составляем систему уравнений:
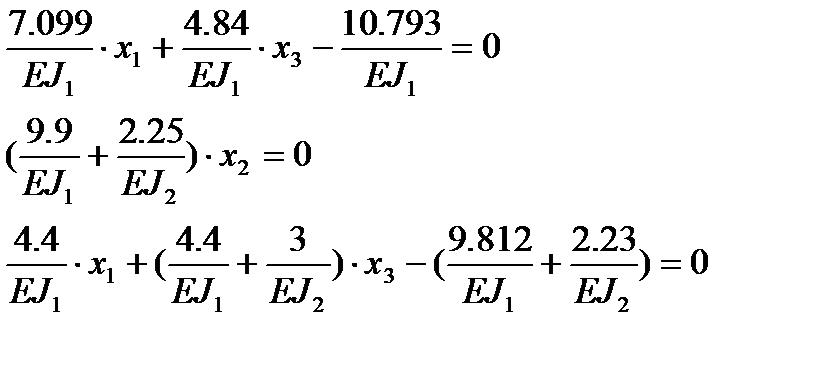
Решив эту систему уравнений получим: х1 = 0.742 кН∙м; х2 = 0; х3 = 1.142 кН∙м. Из уравнений статики определяем опорные реакции для эквивалентной системы (рисунок 5.6), которые одновременно являются опорными реакциями для заданной рамы: НА = 0.742 кН, VА= 3.066 кН, МА = 0.474 кНм, НВ = 0.742 кН, VВ= 3.066 кН, МВ = 0.474 кНм.

Рисунок 5.5 - Эквивалентная система с известными нагрузками и приложенными единичными силами.
По полученным данным строим окончательную эпюру изгибающих моментов (рисунок 5.7)

Рисунок 5.7 - Окончательная эпюра изгибающих моментов.
Проверяем, удовлетворяет ли принятый двутавр условию прочности
 (5.6)
(5.6)
где  – максимальный изгибающий момент, 1.142 кНм (рисунок 5.7);
– максимальный изгибающий момент, 1.142 кНм (рисунок 5.7);
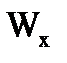 – момент сопротивления относительно оси х,
– момент сопротивления относительно оси х, 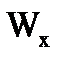 = 184 см3;
= 184 см3;
 – допускаемой напряжение,
– допускаемой напряжение, 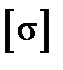 = 158 МПа (см. раздел 2).
= 158 МПа (см. раздел 2).
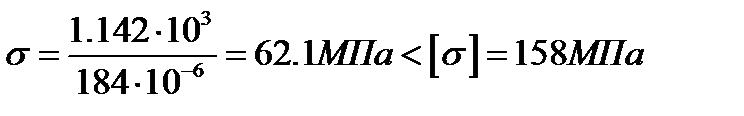
Так как  то условие прочности соблюдается.
то условие прочности соблюдается.
Исходя из технологии сварки условия монтажа учитывая большой запас по прочности приме двутавр №16 таким же, как у ригеля.
По ГОСТ 8239-76 двутавр №16 [5]:
Jx = 873 см4, Jy = 58.6 см4, Wx = 109 см3, Wy = 14.5 см3, ix = 6.57 см, iУ = 1.7 см, Sx= 62.3 см2, h = 160 мм, b = 81 мм, d = 5 мм, t = 7.8 мм, R = 8.5 мм, A = 20.2 см2, Gп.м. = 15.9 кг.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| КП 00 00 00 06 ПЗ |
| Разраб. |
| Куцко |
| Провер. |
| Новосельская |
| Реценз. |
| Н. Контр. |
| Утверд. |
| Новосельская |
| Расчет стоек, проверка на гибкость |
| Лит. |
| Листов |
| БГТУ 4 17 08 17 13 |
При центральном сжатии прямого стержня прямолинейная форма его равновесия устойчива до достижения сжимающей силой так называемого критического значения.
Проверка сжатого стрежня на устойчивость определяется по формуле:
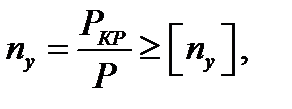 (6.1)
(6.1)
где ny - коэффициент запаса устойчивости;
Pкр — критическое значение сжимающей силы, Н;
Р - сила, сжимающая стержень, Н;
[ny] - допускаемое значение коэффициента запаса устойчивости.
При потере устойчивости с упругой стадии работы стержня критическая сила определяется по формуле Эйлера:
 (6.2)
(6.2)
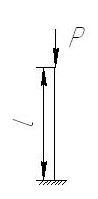
Рисунок 6.1 - Центральное сжатие прямого стержня,проверка на гибкость.
где - Е - модуль упругости материала, Е = 2.1·105 МПа;
Jmin - минимальный главный центральный момент инерции поперечного сечения стойки, м4;
l - длина стойки, м;
μ - коэффициент приведения длины, величина которого для стержня постоянного поперечного сечения зависит от типа и расположения опор. Для данной схемы μ = 2.
Тогда критическое значение сжимающей силы составит:
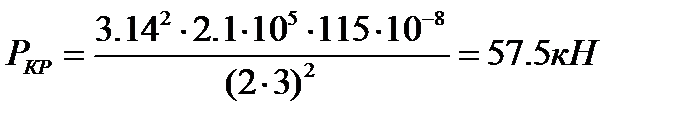
Формула для критического напряжения имеет вид:

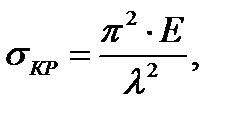 (6.3)
(6.3)
где λ –гибкость стойки:
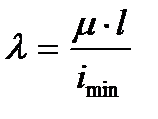 (6.4)
(6.4)
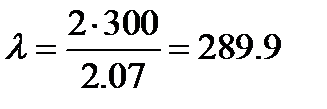
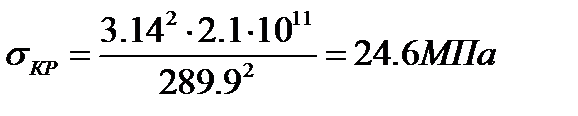
Формула Эйлера применима лишь в пределах действия закона Гука, т.е. при условии, что критическое напряжение не превышает предела пропорциональности материала стержня (σпц = 210 МПа):
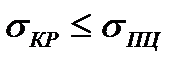 (6.5)
(6.5)
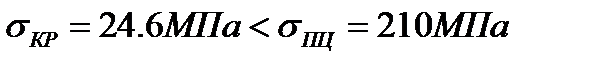
Т.е. условие выполняется.
Из выражения (6.3) и (6.4) следует, что формула Эйлера применима при условии;
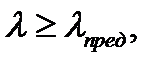 (6.6)
(6.6)
где - λ — гибкость рассчитываемого стержня, зависящая от его приведенной длины (μl), размеров и формы поперечного сечения;
λпред - предельная (граничная) гибкость для материала стержня, зависящая только от физико-механических свойств материала.

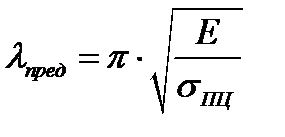 (6.7)
(6.7)

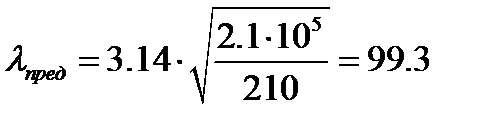
Т.е. условие гибкости выполняется т.к. λ = 289.9 > λпред = 99.3.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| КП 00 00 00 07 ПЗ |
| Разраб. |
| Куцко |
| Провер. |
| Новосельская |
| Реценз. |
| Н. Контр. |
| Утверд. |
| Новосельская |
| Подбор и расчет опорных баз |
| Лит. |
| Листов |
| БГТУ 4 17 08 17 13 |
Проектируемая рама опирается на фундамент при помощи опор, состоящих из набора косынок, приваривающихся к опорной плите и стойке рамы. Рама крепится к фундаменту при помощи фундаментных болтов. На опоры действуют значительные осевые силы возникающие от веса металлоконструкции с грузом, которые приводит к возникновению больших напряжений и реакций фундамента.
Целью расчета является определение толщин опорной плиты и косынок исходя из напряжений сжатия, а также диаметра болтов, крепящих раму к фундаменту.
Расчет производим согласно методике изложенной в [3].Расчетная схема представлена на рисунке 7.1

Рисунок 7.1 - Схема опоры для крепления рамы к фундаменту
Толщину опорной плиты определяем по формуле
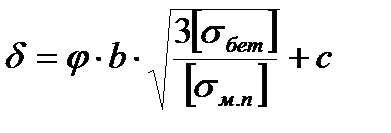 , (7.1)
, (7.1)
где 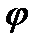 -коэффициент, учитывающий увеличение жесткости при укреплении опорной поверхности ребрами. Находится из следующих соотношений:
-коэффициент, учитывающий увеличение жесткости при укреплении опорной поверхности ребрами. Находится из следующих соотношений:
при  , (7.2)
, (7.2)
при 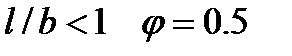 , (7.3)
, (7.3)
где l -расстояние между косынками, l=100 мм (рис. 7.1);
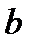 - вылет опорной плиты, b=60 мм.
- вылет опорной плиты, b=60 мм.
Следовательно l/b=100/60=1.33<4 тогда 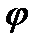 =0,5
=0,5
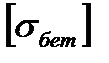 - допускаемой напряжение для бетона М200,
- допускаемой напряжение для бетона М200, 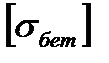 =8МПа;
=8МПа;
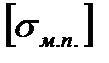 - допускаемое напряжение материала плиты,
- допускаемое напряжение материала плиты, 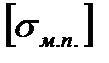 =158 МПа
=158 МПа
с – конструкционная добавка, учитывающая коррозию, с=3 мм.
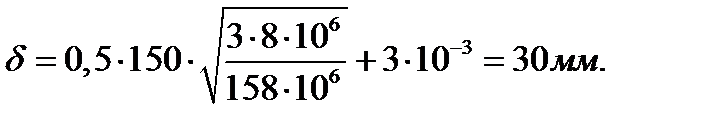
Определяем толщину косынки:
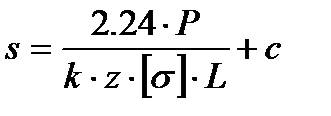 , (7.4)
, (7.4)
где Р – расчетная нагрузка на одну опору, P = 6133,05 Н;
k – коэффициент гибкости, первоначально принимаем k=0.6;
z – число косынок, z=8;
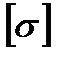 - допускаемое напряжение материала косынки,
- допускаемое напряжение материала косынки, 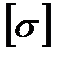 = 158 МПа;
= 158 МПа;
L – длина катета косынки, L=165 мм.

Принимаем косынку со стандартной толщиной s=4 мм.
Определим диаметр болтов, крепящих опору к фундаменту:
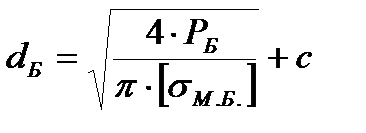 , (7.5)
, (7.5)
где 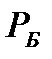 - болтовая нагрузка, Н;
- болтовая нагрузка, Н;
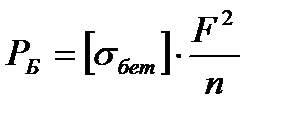 (7.6)
(7.6)
где F - площадь опорной плиты;
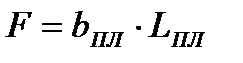
bПЛ – ширина плиты, принимаем равной 340 мм;
LПЛ – длина плиты, принимаем равной 240 мм.
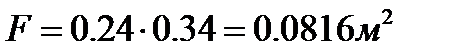
n - количество болтов, крепящих опору к фундаменту. Принимаем n=4;
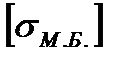 - допускаемое напряжение материала болта,
- допускаемое напряжение материала болта, 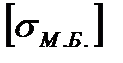 =140 МПа.
=140 МПа.

Следовательно:
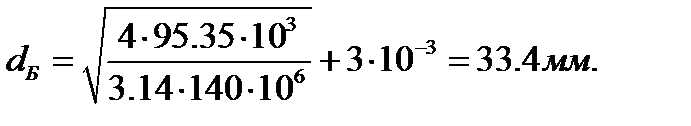
Принимаем фундаментный болт стандартного диаметра БОЛТ М36x4 ГОСТ 7898-70.
Проверяем сварные швы на срез в месте крепления косынки к стойке. Для этого должно соблюдаться следующее условие
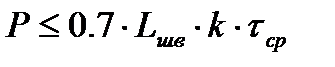 , (7.7)
, (7.7)
где Lшв - периметр всех сварных швов, Lшв=2400 мм;
k - катет сварного шва, k=4 мм;
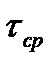 - допускаемое напряжение среза, МПа;
- допускаемое напряжение среза, МПа;
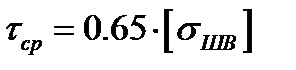 . (7.8)
. (7.8)
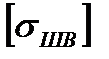 - допускаемое напряжение в сварном шве равное 158 МПа
- допускаемое напряжение в сварном шве равное 158 МПа
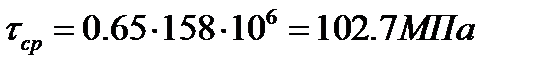
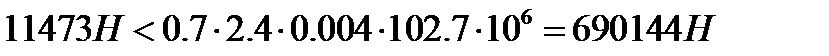
Условие прочности сварных швов соблюдается.
Изм.
Лист
№ докум.
Подпись
Дата
Лист
КП 00 00 00 08 ПЗ
Разраб.
Куцко
Провер.
Новосельская
Реценз.
Н. Контр.
Утверд.
Новосельская
. Степень унификации и стандартизации
Лит.
Листов
8. Степень унификации и стандартизации БГТУ
4 17 08 17 13
Степень унификации и стандартизации определяется коэффициентом унификации (стандартизации) который зависти от числа стандартных деталей металлоконструкции, и определяется как
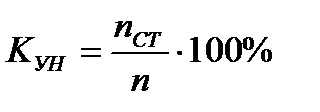 , (8.1)
, (8.1)
где 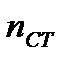 - число стандартизированных и унифицированных деталей и узлов конструкции, шт.;
- число стандартизированных и унифицированных деталей и узлов конструкции, шт.;
 - общее число деталей и узлов конструкции, шт..
- общее число деталей и узлов конструкции, шт..
Количество унифицированных деталей и узлов: опоры – 4 шт.; стойки – 4шт.; ригели – 4 шт.
Количество стандартизированных деталей и узлов: болты – 16 шт.; гайки – 16 шт.; прокладки – 32 шт.
Остальные: косынки – 32 шт.; траверсы – 8 шт.; плиты опорные – 4 шт.
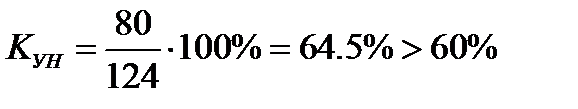
Заключение
В данной работе сконструирована рама с подвижной нагрузкой, произведены расчеты профиля сечения ригеля, стоек. Осуществлен расчет ригеля на выносливость, общую и местную устойчивость и в результате вышеприведенных проверочных расчетов установлено, что данная стержневая конструкция (рама) при заданных нагрузках, размерах и сечениях стержней является достаточно прочной, устойчивой и жесткой в опасных сечениях, а также не разрушается от действия циклических нагрузок за период эксплуатации.
В качестве ригеля принят двутавр №16. В качестве стояк, исходя из равенства моментов инерции сопротивления предлагаемых деталей и методов расчета, так же двутавр №16. Подобраны опоры, и даны рекомендации по установке рамы на площадку.
Приведен список использованных источников и ГОСТов.
Date: 2015-09-22; view: 495; Нарушение авторских прав