Типичные распределения непрерывного типа, используемые в радиотехнике и связи

7.1РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ

Плотность равномерного распределения:

0, если x<=a, x>=b

f(x)=

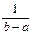, если x € (a,b)

Функция равномерного распределения:

0, если x<=a

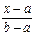, если a<x<=b

F(x)=

1, если x>b

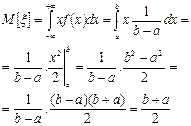
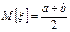
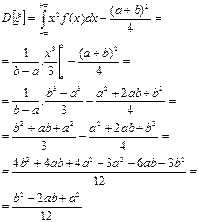
Среднеквадратическое отклонение:

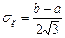
Вероятность попадания в промежуток:

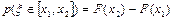
7.2 ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ

(ЭКСПОТЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ)

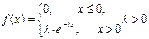
Найдем функцию распределения:

1) x<=0 F(x)=0

2) x>0

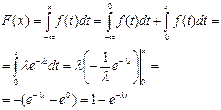
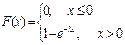
Математическое ожидание:

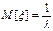
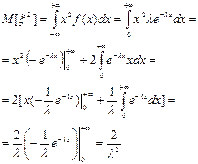
Начальный момент второго порядка:

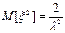
Дисперсия:

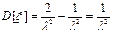
Среднеквадратическое отклонение:

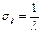
Коэффициент ассиметрии:

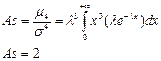
Коэффициент эксцесса:

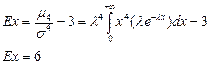
m₃ = 2/λ³ m₄ = 9/λ⁴

Вероятность попадания на промежуток (α, β) или (α, β] или [α, β].

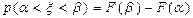
Правило трех сигм для показательного распределения.

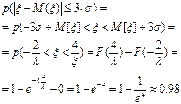
7.3 Нормальное распределение (закон Гаусса)

7.3.1 ВСПОМОГАТЕЛЬНЫЙ МАТЕРИАЛ ИНТЕГРАЛ ЭЙЛЕРА

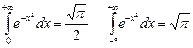
ФУНКЦИЯ ЛАПЛАСА

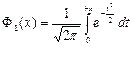
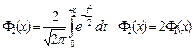интеграл вероятности Функция ошибок Гаусса

Свойства Ф₁ (х)

1) Ф₁ (0) = 0

2) Ф₁ (- х) = - Ф(х)

3)

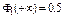
Доказательство:

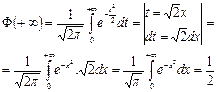
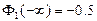
7.3.2 ПЛОТНОСТЬ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

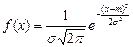
Докажем, что это действительно является плотностью. Должно быть выполнено условие нормировки для плотности.

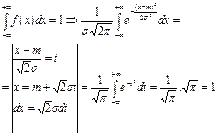
7.3.3 ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

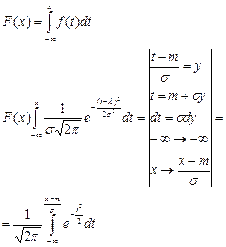
Полученный интеграл делим на два интеграла:

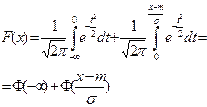
Получается:

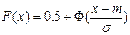
7.3.4. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ.

М(ξ)=m

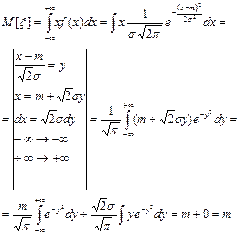7.3.5 ДИСПЕРСИЯ.

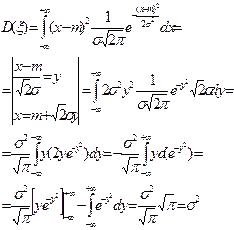
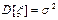
Вероятностный смысл параметра σ – это среднеквадратическое отклонение.

7.3.6 МОДА, МЕДИАНА.

Медиана – это решение уравнения F(x)=0.5.

Мода Мо=m (из чертежа)

Единственный закон распределения, у которого равны мат.ож., мода и медиана это нормальный закон.

7.3.7. ЦЕНТРАЛЬНЫЕ МОМЕНТЫ ЛЮБОГО ПОРЯДКА.

μ_K(ξ) = (k-1)σ²μ_k-2 – рекурентная формула

μ₀=1 μ₁ =0 μ₂ = σ² μ₃ = 0 μ₄ = 3σ⁴

условия нормировки.

Коэффициент ассиметрии:

As=0

Коэффициент эксцесса:

Ex=0

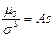
7.3.8. ВЕРОЯТНОСТЬ ПОПАДАНИЯ НА ПРОМЕЖУТОК (α,β)

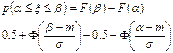
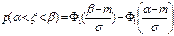
вероятность попадания на симметричный относительно математического ожидания промежуток

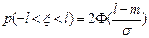
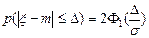
7.3.9. КВАНТИЛИ.

Квантиль уровня р:

F(x)=p

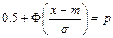
«Случайные векторы(системы случайных величин)»

Date: 2015-09-18; view: 380; Нарушение авторских прав