Плотность распределения СВ непрерывного типа

Если существует функция f(x), интеграл от которой в промежутке от - ∞ до х дает функцию распределения F(x), то эта функция f(x) называется плотностью распределения СВНТ

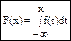
Свойства.

f(x) = F`(x) 2) f(x) ≥ 0

p(x1 ≤ ξ ≤ x2) =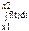

3) 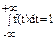- условие нормировки.

4) p(ξ = x) = 0

Числовые характеристики случайных величин.

4.1. Математическое ожидание.

Вероятностный смысл математического ожидания – наиболее вероятное событие в данном случайном процессе.

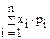для СВДТ

М(ξ) =

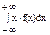для СВНТ

Свойства математического ожидания:

М(а·ξ – b) = a·M(ξ) + b;

M(ξ1 + ξ2) = M(ξ) + M(ξ);

M(ξ1·ξ2) = M(ξ1)·M(ξ2)

4.2..Дисперсия случайной величины

D(ξ)=М[ξ – M(ξ)]2 (М(М(ξ)) = М(ξ)

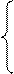
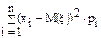- СВДТ.

D(x)=

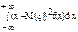-СВНТ.

Свойства:

1) D(С)=0.

2) D(С·x) = С2·D(x)

3) D(а·x + b)=а2·D(x)

4) D(x) = М(x2) - М2(x)

5) D(x1 + x2) = D(x1) + D(x2)

6) D(x1 - x2) = D(x1) + D(x2).

4.3.Среднеквадратичное отклонение

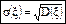(2.7)

Свойства:

σ(С) = 0 2)σ(С·x) = С·σ(x)

3)σ(x1+x2) =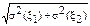

ξ			….	m
p			…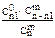

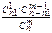
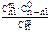
Если случайные события ξ1, ξ2, …, ξn независимы и имеют одно и тоже среднеквадратичное отклонение, то:

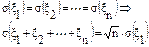
Date: 2015-09-18; view: 358; Нарушение авторских прав