Действия над вероятностями

Операции над событиями (Алгебра событий).

Пересечением двух событий А ÇB называется событие С, когда А и В происходят одновременно [А*В=С (и)-умножение событий]

Несовместные события -A*B=Æ

Сумма событий –(С=А È В, С=А+В)

А + W = W; А + Æ = А

Разность событий –(А-В=С), (А\В=А-В)

Противоположное событие- Ā.

Противоположные события дополняются до полного пространства событий.

Классическое определение вероятности события.

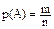(1.1)

Где m-чмсло элементарных исходов испытания, благоприятствующих появлению события А; n-общее число возможных элементарных исходов испытания.

3) Частость наступления события. (Статистическое определение вероятности.)

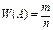
Действия над вероятностями

A) Условная вероятность

Условной вероятностью наступления события А при условии, что произошло событие В

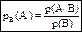(1.2)

B) Формула умножения вероятностей

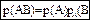(1.3)

Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило

C) Вероятность произведения независимых событий

Два события называются независимыми, если вероятность второго события не зависит от того, произошло или нет первое событие.

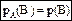
(1.4)

D) Вероятность появления хотя бы одного события.

Пусть событие А состоит в том, что оно произойдет, если произойдет хотя бы одно из событий А1, А2, …, Аn. Тогда противоположное событие Â состоит в том, что ни одно из этих событий не произойдет. Ā=Ā1·Ā2·...·Ān.

Пусть вероятность появления каждого события Аi равно рi, тогда вероятность появления противоположного события будет равна:

Следовательно,

р(А)=1-q1·q2·q3·…·qn

Допустим, что все вероятности равны между собой (р=р1=р2=р3=…рn), тогда: p(A)=1-qn (1.5)

E) Формула сложения вероятностей.

Вероятность появления хотя бы одного из двух совместных событий А и В.

р(А+В)=р(А)+р(В)-р(А·В) (1.6)

Следствие: А·В=Æ. Р(А+В)=р(А)+р(В)

G) Формула полной вероятности.

Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий Н1, Н2, …, Нn, образующих полную группу, арвна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А.

Н1, Н2, …, Нn Эти события называются гипотезами и их вероятности р(Нi) называются априорными (оценочными) А

Н1+Н2+…+Нi=U

А: А=Н1·А+Н2·А+…+Нn·А, тогда

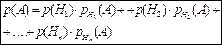(1.7)

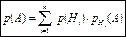
-формула полной вероятности

F) Формула Байеса – учитывает вероятность уже относительно произведенного опыта

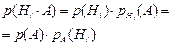
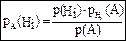(1.8)