Облако 1з-электрона

На рис. изображены значения волновой функции Ѱ (рис. а) и ее ква­драта (рис. б} для 1s-электрона в зависимости от расстояния от ядра г.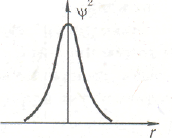

Изображенные кривые не зависят от направления, в котором откладывает­ся измеряемое расстояние г; это означает, что электронное облако 1s -электрона обладает сферической симметрией, т. е. имеет форму шара. Кривая на рис. а расположена по одну сторону от оси расстояний (ось абсцисс). Отсю­да следует, что волновая функция 1s-электрона обладает постоянным знаком; будем считать его положительным.

Рис. б показывает также, что при увеличении расстояния от ядра величи­на Ѱ² монотонно убывает. Это означает, что по мере удаления от ядра плотность электронного облака 1s-электрона уменьшается.

Из этого не следует, однако, что с ростом r вероятность обнаружить 1s-электрон тоже монотонно убывает. На следующем рис. выделен тонкий слой, заключенный между сферами с радиусами r и (r + Δ r), где Δ r — некоторая малая величина.

С ростом r плотность электронного облака в рассматриваемом сферическом слое уменьшается; но одновременно возрастает объем этого

слоя, равный 4 r²Δr. Как уже говорилось, вероятность обнаружить электрон в малом объеме ΔV выражается произведением Ѱ²ΔV, В данном случае ΔV = 4 r²Δr; следова­тельно, вероятность обнаружения электрона в сферическом слое, заключенном между r и (r + Δ r), пропорциональна величине 4 r² Ѱ². В этом произведении с увеличением r множитель 4 r² возрастает, а множитель Ѱ² убывает. При малых значениях r величина 4 r² возрастает быстрее, чем убывает Ѱ², при больших — наоборот. Поэтому произведение 4 r² Ѱ², характеризующее вероятность обна­ружения электрона на расстоянии r от ядра, с увеличением r проходит через максимум.

Зависимость величины 4 r² Ѱ² от r изображена для 1s-электрона на рис. (подобные графики называются графиками радиального распределения вероят­ности нахождения электрона).

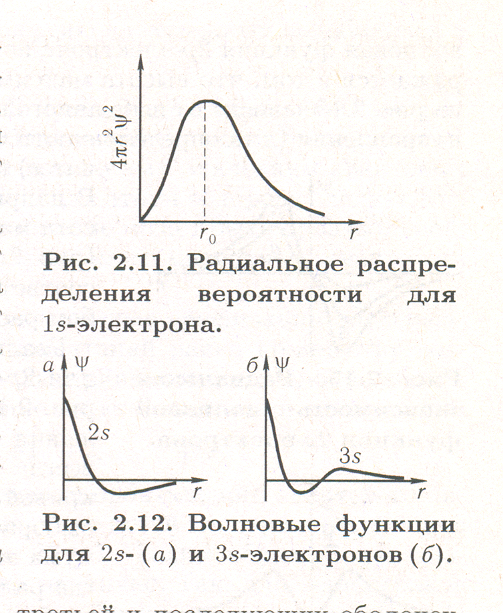
Как показывает рис.2.11, вероятность об­наружить 1s-электрон на малых расстояни­ях от ядра близка к нулю, так как r мало. Ничтожно мала и вероятность обнаружения электрона на очень большом расстоянии от ядра: здесь близок к нулю множитель Ѱ² (см. рис. ранее ). На некотором расстоянии от ядра r₀ вероятность обнаружения электрона имеет максимальное значение. Для атома водорода это расстояние равно 53 пм, что совпадает с вычисленным Бором значением радиуса ближайшей к ядру орбиты электрона. Одна­ко трактовка этой величины в теории Бора и с точки зрения квантовой механики различ­на: согласно Бору, электрон в атоме водоро­да находится на расстоянии 53 nm от ядра, а с позиций квантовой механики этому рас­стоянию соответствует лишь максимальная вероятность обнаружения электрона.

Электронные облака s-электронов второй, третьей и последующих оболочек обладают, как и в случае 1s-электронов, сферической симметрией, т. е. харак­теризуются шарообразной формой. Однако здесь волновая функция при уве­личении расстояния от ядра меняется более сложным образом. Как показывает рис. 2.12, зависимость Ѱ от r для 2s- и Зs-электронов не является монотонной, на разных расстояниях от ядра волновая функция имеет различный знак, а на со­ответствующих кривых есть узловые точки (или узлы), в которых значение вол­новой функции равно нулю. В случае 2s-электрона имеется один узел, в случае 3s-электрона — 2 узла и т. д. В соответствии с этим, структура электронного облака здесь также сложнее, чем у 1s-электрона. На рис. 2.13 в качестве примера схематически изображено электронное облако 2s-электрона.

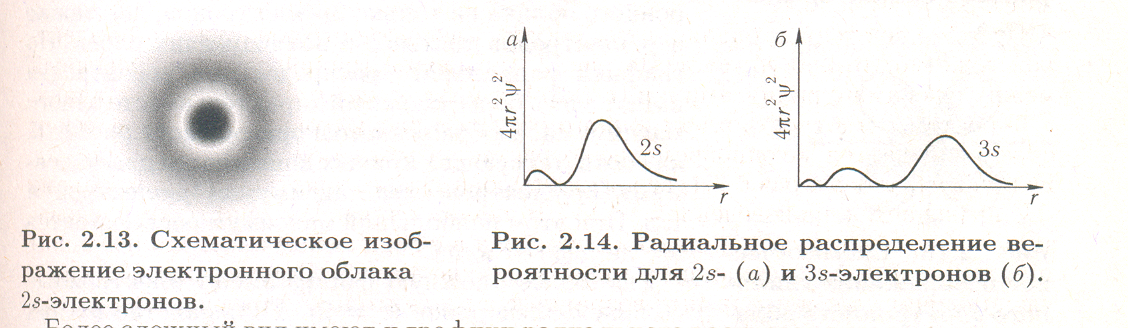Более сложный вид имеют и графики радиального распределения вероятности для 2s- и 3s-электронов (рис. 2.14). Здесь появляется уже не один максимум, как в случае 1s-электрона, а соответственно два или три максимума. При этом главный максимум располагается тем дальше от ядра, чем больше значение главного квантового числа n.

Рассмотрим теперь структуру электронного облака 2p-электрона. При удале­нии от ядра по некоторому направлению волновая функция 2p-электрона изме­няется в соответствии с кривой, изображенной на рис. 2.15, а.

По одну сторону от ядра (на рисунке — справа) волновая функция положи­тельна, и здесь на кривой имеется максимум, по другую сторону от ядра (на ри­сунке — слева) волновая функция отрицательна, на кривой имеется минимум; в начале координат значение Ѱ обращается в нуль. В отличие от s-электронов, волновая функция 2р-электрона не обладает сферической симметрией. Это вы­ражается в том, что высота максимума (и, соответственно, глубинаминимума) на рис, 2.15 зависит от выбранного направления радиуса-вектора r. В некотором направлении (для определенности будем считать его направлением оси коорди­нат х) высота максимума наибольшая (рис. 2.15, а). В направлениях, составляющих угол с осью х, вы­сота максимума тем меньше, чем больше этот угол (рис. 2.15, б, в); если он равен 90°, то значение Ѱ в соответствующем направлении равно нулю при лю­бом расстоянии от ядра.

График радиального распределения вероятности для 2р-электрона (рис. 2.16) имеет вид, сходный с рис. 2.15, с той разницей, что вероятность обнаружения электрона на некотором расстоянии от ядра всегда положительна. Положение максимума на кривой распределения вероятности не зависит от выбора направления. Однако высота этого макси­мума зависит от направления: она наибольшая, ко­гда радиус-вектор совпадает с направлением оси x, и убывает по мере отклонения радиуса-вектора от этого направления.

Такому распределению вероятности обнаружения 2р-электрона соответствует форма электронного об­лака, напоминающая двойную грушу или гантель (рис. 2.17).

Как видно, электронное облако сосредоточено вблизи оси х, а в плоскости yz, перпендикулярной этой оси. электронного облака нет; вероятность об­наружить здесь 2р-электрон равна нулю.

Рис. 2.17 приближенно передает форму элект­ронного облака не только 2р- электронов, но также и р-электронов третьего и последующих слоев. Но графики радиального распределения вероятности имеют здесь более сложный характер: вместо одного максимума, изображенного в правой части рис. 2.16, на соответствующих кривых появляются два макси­мума (Зр-электрон), три максимума (4р-электрон) и т. д. При этом наибольший максимум располагается все дальше от ядра.

Еще более сложную форму имеют электронные облака d -электронов ( l = 2). Большинство из них представляют собой «четырехлепестковую» фигуру (рис. 2.18).

Если несколько электронов имеют одинаковые значения и главного, и орби­тального квантовых чисел (комбинацию (n,l)), то говорят, что они относятся к одной электронной подоболочке, энергетическому подуровню, квантовому под­слою:

(п; I) = const — электронная подоболочка, энергетический подуровень, кван­товый подслой.

Исходя из значений п и l, возможны следующие типы электронных подоболочек:

1 s, 2 s, 2 р, 3 s, З р, 3 d, 4 s, 4 р, 4 d, 4 f, 5 s, 5 р, 5 d, 5 f, 5 g, 6 s, 6 p, 6 d,...

Орбитальное квантовое число влияет на энергию электронных подоболочек в многоэлектронных атомах.

Магнитное квантовое число. В предыдущих параграфах мы вы­яснили, что размеры и формы электронных облаков в атоме могут быть не любы­ми, а только такими, которые соответствуют возможным значениям квантовых чисел n и l. Из решения уравнения Шредингера для атома водорода следует, что и ориентация электронного облака в пространстве не может быть произвольной: она определяется значением третьего, так называемого магнитного квантового числа m_i.

Магнитное квантовое число определяет возможные ориентации электрон­ного облака в пространстве. Число таких ориентаций равно количеству воз­можных значений магнитного квантового числа, принимающего целочисленные значения, по модулю не превышающие значение орбитального квантового числа:

m_i = -l,..., -2, -1, 0, +1, +2,..., + l.

Всего таких значений для конкретного значения орбитального квантового

чи­сла 2 l + 1. Это означает, что число возможных ориентаций электронных облаков конкретной электронной подоболочки равно 2 l + 1. Таким образом, для раз­ных значений l число возможных значений m_i различно. Так, для s-электронов ( l = 0) возможно только одно значение m_i ( m_i = 0); для р-электронов ( l = 1) возможны три различных значения m_i (—1, 0, +1); при l =2 (d-электроны) m_i может принимать пять различных значений (—2, —1, 0, +1, +2), при l = 3 (f-электроны) m_i может принимать семь различных значений (—3, —2, —1, О, +1,+2,+3).

Квантовое число m_i получило название магнитного, поскольку от его значения зави­сит взаимодействие магнитного поля, создаваемого электроном, с внешним магнитным полем. В отсутствие внешнего магнитного поля энергия электрона в атоме не зависит от значения m_i. В этом случае электроны с одинаковыми значениями n и l, но с разны­ми значениями m_i обладают одинаковой энергией. Однако при действии на электрон внешнего магнитного поля энергия электрона в атоме изменяется, так что состояния электрона, различающиеся значением m_i, различаются и по энергии. Это происходит потому, что энергия взаимодействия магнитного поля электрона с внешним магнитным полем зависит от величины магнитного квантового числа. Именно поэтому в магнит­ном поле происходит расщепление некоторых атомных спектральных линий: вместо одной линии в спектре атома появляются несколько (эффект Зеемана).

Волновая функция, описывающая состояние электрона в атоме, и полностью характеризуемая конкретными значениями квантовых чисел n, I и m_i, называ­ется пространственной атомной орбиталью или просто атомной орбиталъю. Для такой атомной орбитали принято сокращенное обозначение — АО, которым пользуются повсеместно при обсуждении свойств и строения атомов и молекул. Таким образом,

(n, I, m_i)= const — атомная орбиталь, квантовая ячейка.

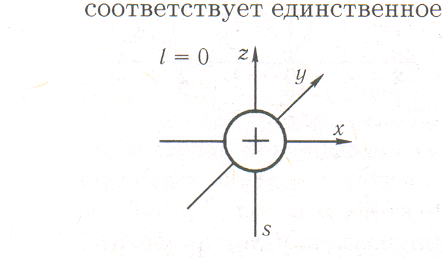
Симметрия атомных орбиталей. Поскольку s-состоянию (l = 0) соответствует единственное значение магнитного квантового числа (m_i = 0), то любые возможные расположения s-электронного облака в пространстве идентичны. Действи­тельно, математическая функция s-типа неиз­менна по отношению к следующим действиям, называемым операциями симметрии: вращению вокруг любой из осей и отражению в любой из плоскостей, проходящих через начало коорди­нат. Для нее также характерна неизменность по отношению к инверсии относительно начала координат (рис. 2.20).

Все перечисленные опе­рации преобразуют систему саму в себя и оста­вляют нетронутой по крайней мере одну точку. Поэтому они называются точечными операци­ями симметрии. Неизменность значений АО в любой точке пространства при преобразованиях (вращение вокруг оси, отраже­ние относительно плоскости, инверсия относительно точки) называется

симметричностью функции. s-АО — симметричная функция, так как при любой из операций симметрии, переводящей точку r₁ в точку r₂, имеет место равенство:

Ѱ(r₁)=Ѱ(r₂).

На рис. 2.21 изображены АО р-симметрии. р-Орбитали характеризуются тре­мя различными значениями m_i; в соответствии с этим они располагаются в про­странстве тремя способами. При этом три р-электронных облака ориентированы во взаимно перпендикулярных направлениях, которые обычно принимают за на­правления координатных осей (x, у или z). Если АО ориентирована вдоль оси х, то она называется р_x-орбиталью; соответственно определяются названия р _y- и р_z-орбиталей. Примечательно то, что при положительных значениях каждой из осей декартовой системы координат соответствующая р-АО положительна, а при отрицательных — отрицательна. Рассмотрим внимательнее отношение к операциям симметрии р_x-АО.

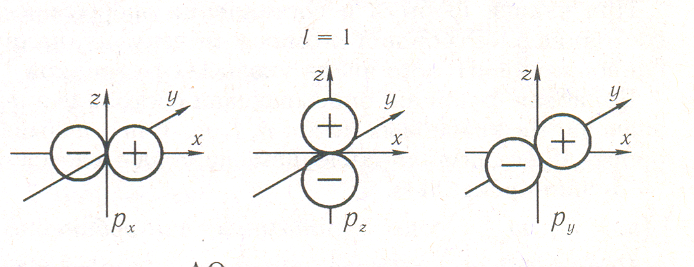
По отношению к вращению вокруг оси х АО симметрична, но по отношению к такой же операции симметрии вокруг оси у или z функция меняет знак. То есть в последнем случае АО совпадет со своим первоначальным изображением, если ее умножить на (—1). Значит, р_x-АО симметрична по отношению к вращению во­круг оси х и антисимметрична по отношению к вращению вокруг оси у или z. Также видно, что р_x-функция симметрична по отношению к отражению в любой из плоскостей, проходящих через ось x, и антисимметрична по отношению к отражению в плоскости уz. Данная орбиталь также антисимметрична к операции инверсии относительно начала координат.

Для d-орбиталей (l =2) возможно уже пять значений магнитного квантового числа и соответственно пять различных ориентации d-электронных облаков в пространстве (рис. 2.22).

/= 2

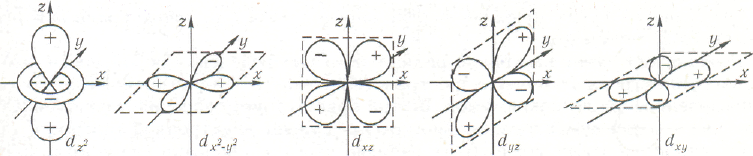
Названия (d-АО и их симметрия находятся в полном соответствии друг дру­гу. Орбиталь с индексом ху ориентирована вдоль диагонали между осями х и у; знак ее в точке пространства с координатами (x, у, z) положителен, если произведение х • у положительно, и наоборот. Аналогично определяется ориен­тация и значность d_xz, d_yz-АО. Орбиталь d_x2-y2 ориентирована вдоль осей х и у. Она положительна в точках пространства, располагающихся вдоль оси х (как и функция х². имеющаяся в подстрочном индексе орбитали) и отрицательна вдоль оси у (как —у²). Функция d_z2 всегда положительна в точках пространства, распо­лагающихся вдоль оси z (подстрочный индекс z² в таких точках положителен). Спиновое квантовое число. Теоретически было показано Дираком, а экспериментально подтверждено исследованиями атомных спектров, что поми­мо квантовых чисел n, l и m_i, электрон характеризуется еще одной квантованной величиной, не связанной с движением электрона вокруг ядра, а определяющей его собственное состояние. Эта величина получила название спинового кванто­вого числа или просто спина (от английского spin — кручение, вращение); спин обычно обозначают буквой т_s.

Спиновое квантовое число отражает наличие у электрона собственного мо­мента движения. Проекция собственного момента количества движения элек­трона на избранное направление (например, на ось z и называется спином. Спи­новое квантовое число принимает два значения:

т_s = +1/2 или -1/2.

При записи формул и составлении энергетических диаграмм, отражающих состояние электронов в атомах и молекулах, наличие того или иного значения спинового квантового числа указывают стрелкой ↑ или ↓.

Волновая функция, описывающая состояние электрона в атоме конкретными значениями квантовых чисел n, l, m_i и m_s, называется спин-орбиталью. Спин-орбиталь с одним направлением спина называется α-спин-орбиталью, а с другим — β-спин-орбиталью.

( n,l,m_i,m_s ) = const — атомная спин-орбиталъ.

Например, Зр_x-орбиталь со спином +1/2 может быть обозначена как Зр_x^α-спин-орбиталь, а 4s-орбиталь со спином — 1/2 тогда обозначают как 4s^β-спин-орбиталь.

Четыре квантовых числа — n, l, m_i, m_s — полностью определяют состояние электрона в атоме.

Date: 2015-09-18; view: 1128; Нарушение авторских прав