
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Квантово-механическая модель атома
|
|
В простейшем из атомов — атоме водорода — потенциальная энергия электрона определяется его кулоновским притяжением к ядру. Поскольку в атомных единицах заряды электрона и ядра равны —1 и +1 соответственно, то
Еп= -  ,
,
где r — расстояние электрона от ядра. Если подставить в уравнениеданное выражение для потенциальной энергии и решить уравнение Шредингера, то можно найти, что распределение электрона по энергиям и в пространстве атома водорода определяется волновой функцией Ѱ, зависящей от сферических координат (r, 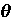 ,
, 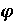 ) электрона и от трех параметров (n, l, mi), принимающих целочисленные значения. Последние три параметра называют квантовыми числами. Это n — главное квантовое число, l — орбитальное квантовое число, mi — магнитное квантовое число. Было показано, что электрон также характеризуется четвертым квантовым числом — спиновым (ms). В простейших приложениях квантовой механики иногда удобнее вместо самой волновой функции пользоваться квантовыми числами, представляющими ее. Такой подход часто применяется для объяснения свойств многоэлектронных атомов.
) электрона и от трех параметров (n, l, mi), принимающих целочисленные значения. Последние три параметра называют квантовыми числами. Это n — главное квантовое число, l — орбитальное квантовое число, mi — магнитное квантовое число. Было показано, что электрон также характеризуется четвертым квантовым числом — спиновым (ms). В простейших приложениях квантовой механики иногда удобнее вместо самой волновой функции пользоваться квантовыми числами, представляющими ее. Такой подход часто применяется для объяснения свойств многоэлектронных атомов.
Главное квантовое число. В многоэлектронных атомах конкретный электрон находится в поле ядра, экранированном полем остальных электронов. С физической точки зрения это можно представить так, что данный электрон «видит» не все ядро атома, а лишь некоторую его часть. Данный заряд ядра, действующий на электрон конкретной орбитали с учетом экранирования ядра другими электронами, называется эффективным зарядом ядра данной орбитали (z*). В этом случае
Еп =- 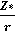
Подставляя данное выражение для Еп в уравнение Шредингера, можно найти, что уравнение имеет решения не при любых, а только при определенных значениях энергии. Таким образом, квантованность энергетических состояний электрона в атоме оказывается следствием присущих электрону волновых свойств. При этом полная энергия электрона в многоэлектронном атоме рассчитывается с помощью выражения:
E=-1/2×(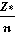 )2
)2
включающего главное квантовое число. Таким образом, главное квантовое число характеризует энергию электрона в атоме. Оно принимает положительные целочисленные значения от 1 до бесконечно больших чисел:
n= 1,2,3,..., 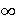 .
.
Наименьшей энергией электрон обладает при n = 1; с увеличением п энергия электрона возрастает. Поэтому состояние электрона, характеризующееся определенным значением главного квантового числа, принято называть энергетическим уровнем электрона в атоме: при п = 1 электрон находится на первом энергетическом уровне, при п = 2 — на втором и т. д. Увеличение значения n ведет к повышению энергии электрона, достигая в пределе нулевого значения. При этом электрон оказывается бесконечно далеко удаленным от ядра и не испытывает к нему какого-либо притяжения. Поэтому, чем меньше значение п, тем отрицательнее энергия электрона, тем более он связан, т. е. испытывает притяжение к ядру, находится в устойчивом состоянии связи с ядром.
При малых значениях n разность энергий ближайших электронных оболочек относительно велика, а при больших значениях n мала. Энергетические уровни с п = 5 и выше настолько близки друг к другу по энергии, что они практически сливаются.
Если электрон атома характеризуется определенным значением энергии Ei, то говорят, что он «находится» на энергетическом уровне Еi. Состояние атома, когда его электроны находятся на таких энергетических уровнях, что их суммарная энергия в атоме является минимальной из возможных значений энергии, называется основным состоянием. Соответствующие состояния электронов также называют основными. Состояния с более высокими значениями энергии называют возбужденными, а сам процесс или результат повышения энергии атома (или электрона) — возбуждением. Главное квантовое число определяет характер радиальной зависимости орбитали, т. е. размеры электронного облака. Чем больше n, тем дальше от ядра атома располагается область наиболее вероятного нахождения электрона. Другими словами, n определяет, средний радиус нахождения электрона в атоме.
О нескольких электронах атома, имеющих одно и то же значение п, говорят, что они относятся к некоторой общей электронной оболочке, энергетическому уровню или квантовому слою:
n=const: электронная оболочка, энергетический уровень, квантовый слой.
Для них, в зависимости от значения n, приняты следующие буквенные обо
значения:
| Главное квантовое число n | |||||||
| Обозначение электронной оболочки (энергетического уровня, квантового слоя) | K | L | M | N | O | P | Q |
Орбитальное квантовое число. В отличие от главного, орбиталь ное квантовое число определяет не радиальную, а угловую зависимость волновой функции, т. е. форму электронного облака. Возможные значения данного числа зависят от значения главного квантового числа и, не превышая значения (n — 1), изменяются в ряду:
l = 0, 1, 2,...,(п-1).
Так же как и энергия, произвольной не может быть и форма электронного облака. Она определяется дискретными значениями орбитального квантового числа l, его называют также побочным, или азимутальным. Различным значениям n отвечает разное число возможных значений l. Так, при n = 1 возможно только одно значение орбитального квантового числа — нуль ( l = 0), при п =2 l может быть равным 0 или 1, при n = 3 возможны значения l, равные 0, 1 и 2, вообще, данному значению главного квантового числа n соответствуют n различных возможных значений орбитального квантового числа.
Вывод о том, что формы атомных электронных облаков не могут быть произвольными, вытекает из физического смысла квантового числа l. Именно, оно определяет значение орбитального момента количества движения электрона, эта величина, как и энергия, является квантованной физической характеристикой состояния электрона в атоме.
Мы уже знаем, что энергия электрона в атоме зависит от главного квантового числа n. В атоме водорода энергия электрона полностью определяется значением n. Однако в многоэлектронныхатомах энергия электрона зависит и от значения орбитального квантового числа l. Поэтому состояния электрона, характеризующиеся различными значениями l, принято называть энергетическими подуровнями электрона в атоме. Этим подуровням присвоены следующие буквенные обозначения:
| Орбитальное квантовое число | ||||||
| Буквенное обозначение орбитального квантового числа | s | p | d | f | g | h |
Электроны, характеризующиеся значениями орбитального квантового числа О, 1, 2 и 3, называют соответственно s -электронами, p -электронами, d -электронами и f -электронами. При данном значении главного квантового числа n наименьшей энергией обладают s -электроны, затем p -, d - и f -электроны.
Состояние электрона в атоме, отвечающее определенным значениям n и l, записывается следующим образом: сначала цифрой указывается значение главного квантового числа, а затем буквой — орбитального квантового числа. Так, обозначение 2 p относится к электрону, у которого n = 2 и l = 1, обозначение З d — к электрону, у которого n = 3 и l = 2.
Электронное облако не имеет резко очерченных в пространстве границ. Поэтому понятие о его размерах и форме требует уточнения. Рассмотрим в качестве примера электронное облако 1 s -электрона в атоме водорода.В точке а, находящейся на некотором расстоянии от ядра, плотность электронного облака определяется квадратом волновой функции Ѱa2. Проведем через точку а поверхность равной электронной плотности, соединяющую точки, в которых плотность электронного облака характеризуется тем же значением Ѱa2 В случае 1 s -электрона такая поверхность окажется сферой, внутри которой заключена некоторая часть электронного облака (на рис. сечение этой сферы плоскостью рисунка изображено окружностью, проходящей через точку а). Выберем теперь точку b, находящуюся на большем расстоянии от ядра, и также проведемчерез нее поверхность равной электронной плотности. Эта
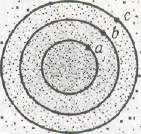
поверхность тоже будет обладать сферической формой, но внутри ее будет заключена несколько большая часть электронного облака, чем внутри сферы а. Пусть, наконец, внутри поверхности равной электронной плотности, проведенной через некоторую точку с, заключена преобладающая часть электронного облака; обычно эту поверхность проводят так, чтобы она заключала 90% заряда и массы электрона. Такая поверхность называется граничной поверхностью, и именно ее форму и размеры принято считать формой и размерами электронного облака. Граничная поверхность 1s-электрона представляет собой сферу, однако граничные поверхности p- и d -электронов имеют более сложную форму.
Date: 2015-09-18; view: 1040; Нарушение авторских прав