Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Дифференциальное уравнение теплопроводности. Условия однозначности
|
|
Распределение температуры в теле, описывается дифференциальным уравнением теплопроводности, которое при принятых допущениях, а именно: тело однородно и изотропно; физические параметры тела постоянны во времени и пространстве; температурные деформации рассматриваемого элементарного объема малы по сравнению с самим объемом; внутренние источники теплоты распределены в рассматриваемом объеме равномерно; макрочастицы тела неподвижны относительно друг друга; имеет следующий вид:
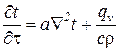
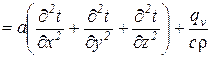, где 
– время, сек;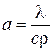 
– коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела, 
;
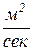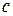– теплоемкость тела; 
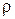– плотность тела; 
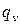– объемная плотность тепловыделения, вm/м3; 
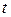– температура; 
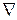– оператор Лапласа.
Условия однозначности:
I) Геометрические условия (форма, размеры тела);
II)Физические условия (физические свойства тела и его физические параметры);
III) Начальные условия (распределение температуры в теле в начальный момент времени);
IV) Граничные условия, определяющие взаимодействие тела с окружающей средой.
1. Граничные условия первого рода. Задается распределение температуры на поверхности тела, как функция координат и времени: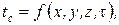 
2. Граничные условия второго рода. Задается распределение плотности потока на поверхности тела, как функция координат и времени: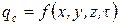 
В частном случае, когда плотность теплового потока на поверхности тела остается постоянной, имеем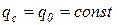 
.
3. Граничные условия третьего рода. Задается температура окружающей среды 
и закон теплообмена между поверхностью тела и окружающей средо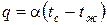й: 
если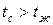 
, где 
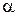– коэффициент теплообмена, представляющий собой плотность теплового потока подведенного (отведенного) к единице поверхности тела при разности температур между поверхностью тела и окружающей среды 1 0С, вm/м2град.
4. Граничные условия четвертого рода. Отражают условия теплообмена системы тел имеющих различные коэффициенты теплопроводности. Между телами предполагается идеальный контакт. Тогда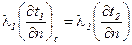 
, где 
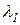– коэффициент теплопроводности первого тела; 
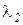– коэффициент теплопроводности второго тела.
Date: 2015-09-18; view: 747; Нарушение авторских прав