
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Контрольная работа по курсу
|
|
«Введение в математический аппарат квантовой механики».
Тема: Линейные операторы. Спектр операторов.
Вариант 2
1. Пусть  и
и 
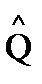 - коммутирующие ортогональные проекторы. При каких
- коммутирующие ортогональные проекторы. При каких 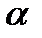 и
и 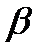 оператор
оператор 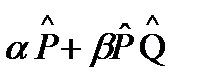 также является ортогональным проектором?
также является ортогональным проектором?
2. Эрмитов оператор 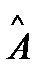 в некотором гильбертовом пространстве удовлетворяет уравнению
в некотором гильбертовом пространстве удовлетворяет уравнению  3+
3+  2=6
2=6  . Найдите собственные значения этого оператора.
. Найдите собственные значения этого оператора.
3. Оператор 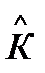 задан в вещественном гильбертовом пространстве функций, квадратично интегрируемых на полупрямой
задан в вещественном гильбертовом пространстве функций, квадратично интегрируемых на полупрямой 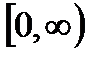
К(х,у)= 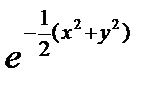
Найдите его собственные значения и нормированные собственные функции
Указание: воспользуйтесь формулой


б) критерии оценивания компетенций (результатов):
Оценка «отлично» - задания контрольной работы выполнены более чем на 80%, продемонстрировано уверенное знание теоретических положений, допустимо наличие в решениях несущественных неточностей. Оценка «хорошо» - задания контрольной работы выполнены более чем на 2/3, при этом продемонстрированы прочные знания учебного материала, однако, решения содержат определенные (несущественные) неточности. Оценка «удовлетворительно» - задания контрольной работы выполнены более чем на 50%, знание учебного материала-посредственное. Оценка «неудовлетворительно» - решено менее 50% заданий, в решении задач имеются существенные ошибки, продемонстрировано незнание значительной части учебного материала.
в) описание шкалы оценивания:
Оценка «отлично»- 26-30 баллов
Оценка «хорошо»- 21-25 баллов
Оценка «удовлетворительно»-15-20 баллов
Оценка «неудовлетворительно»-меньше 15 баллов
6.3. Методические материалы, определяющие процедуры оценивания знаний, умений, навыков и (или) опыта деятельности, характеризующих этапы формирования компетенций
Рейтинговая оценка знаний является интегральным показателем качества теоретических и практических знаний и навыков студентов по дисциплине и складывается из оценок, полученных в ходе текущего контроля и промежуточной аттестации.
Текущий контроль в семестре проводится с целью обеспечения своевременной обратной связи, для коррекции обучения, активизации самостоятельной работы студентов.
Промежуточная аттестация предназначена для объективного подтверждения и оценивания достигнутых результатов обучения после завершения изучения дисциплины.
Текущий контроль осуществляется два раза в семестр: контрольная точка № 1 (КТ № 1) и контрольная точка № 2 (КТ № 2).
Результаты текущего контроля и промежуточной аттестации подводятся по шкале балльно-рейтинговой системы.
| Вид контроля | Этап рейтинговой системы Оценочное средство | Балл | |
| Минимум | Максимум | ||
| Текущий | Контрольная точка № 1 | ||
| Оценочное средство №1.1 Контрольная работа | |||
| Контрольная точка № 2 | |||
| Оценочное средство № 2.1 Контрольная работа | |||
| Промежуточный | Зачет | ||
| Оценочное средство Вопросы к зачету | |||
| ИТОГО по дисциплине |
7. Перечень основной и дополнительной учебной литературы, необходимой для освоения дисциплины
а) основная учебная литература:
1.Мултановский В.В., Василевский А.С. Квантовая механика.-М., Дрофа.2007.-400 с. (ЧЗ(2), ХР (48)).
2.Флюгге З. Задачи по квантовой механике. Изд-во ЛКИ, 2010.-344с. (Ч(3), ХР(8)).
3. Матвеев А.Н. Атомная физика.-М., ОНИКС.2007.-432 с. (ЧЗ(2), ХР(3)).
б) дополнительная учебная литература:
1. Рихтмайер Р. Принципы современной математической физики.-М., Изд.-во «Мир».-1982.-486с.
2.Вулих Б.З. Введение в функциональный анализ.-М.,Изд-во «Наука».-1967.-413с.
3.Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа.-М.,Изд-во «Наука».-1989.-623с.
4. Балашов В.В., Долинов В.К. Курс квантовой механики.-Ижевск, Изд-во РХД, 2001г.-122с.(ЧЗ(2) ХР(21)).
5. А. Мессиа. Квантовая механика. Т. 1,2.- М., Наука, 1979 – ЧЗ(2), ХР(4).
6.Садбери А. Квантовая механика и физика элементарных частиц.-М., Мир.-1989г.-481 с.(ХР(3)).
7.Елютин П.В., Кривченков В.Д. Квантовая механика.-М., Наука.-1976.-332 с.
8. Перечень ресурсов информационно-телекоммуникационной сети «Интернет» (далее - сеть «Интернет»), необходимых для освоения дисциплины
1.http://www.iqlib.ru/ Электронная библиотека IQLb образовательных и просветительских изданий. Свободный доступ к электронным учебникам, справочным и учебным пособиям.
2.http://www/edu/ru/modules/php?op=modload&name=Web_.Links&file=index&l_op=viewlk&cid=2720 – Федеральный портал российского профессионального образования: Математика и естественно-научное образование.
9. Методические указания для обучающихся по освоению дисциплины
Дисциплина «Введение в математический аппарат квантовой механики» состоит из двух основных частей:
1.Элементы теории гильбертовых пространств.
2.Элементы теории линейных операторов в гильбертовых пространствах.
Теория гильбертовых пространств, изложению которой предшествует изложение аппарата линейных (векторных) пространств, имеет непосредственное отношение к постулату состояний квантовой системы. При изучении этого раздела особое внимание рекомендуется обратить на разложение произвольного элемента гильбертова пространства (вектора состояния квантовой системы) по ортонормированному базису (разложение Фурье) и интерпретацию коэффициентов Фурье как амплитуд вероятности (в случае, когда вектор состояния нормирован на единицу). Последнее свойство коэффициентов Фурье используется в проекционном постулате квантовой механики (постулате Дирака-Швингера), описывающем процедуру (однократного) измерения некоторой наблюдаемой. Кроме этого, рекомендуется обратить внимание на классические ортогональные полиномы, используемые в квантовой механике: полиномы Эрмита (используются в задаче о квантовании линейного гармонического осциллятора), полиномы Лежандра (используются в теории углового момента) и полиномы Лягерра (используются в квантовомеханической задаче Кеплера).
Элементы теории линейных операторов в гильбертовых пространствах используются при формулировании постулата наблюдаемых. При изучении этого раздела особое внимание рекомендуется обратить на понятие эрмитова (самосопряженного) оператора и теорему Рисса-Фреше, с помощью которой устанавливается существование оператора, эрмитово сопряженного к ограниченному линейному оператору. Кроме того, в задаче о квантовании уровней квантовой системы важную роль играет понятие спектра оператора и связанных с ним понятий собственных значений и собственных функций и обобщенных собственных значений и собственных функций эрмитова оператора, на которые также рекомендуется обратить особое внимание.
10. Перечень информационных технологий, используемых при осуществлении образовательного процесса по дисциплине, включая перечень программного обеспечения и информационных справочных систем (при необходимости)
10.1 Перечень информационно-справочных систем
Google академия. https://scholar.google.ru (раздел: Физика)
Единое окно доступа к информационным ресурсам. window.edu.ru
11. Описание материально-технической базы, необходимой для осуществления образовательного процесса по дисциплине
При осуществлении образовательного процесса по данной дисциплине используется аудитория С-322, оснащенная мультимедийным оборудованием, оборудованная 10 компьютерами.
12. Иные сведения и (или) материалы
12.1. Перечень образовательных технологий, используемых при осуществлении образовательного процесса по дисциплине
Для достижения планируемых результатов при изучении дисциплины используются следующие образовательные технологии:
1.Информационно-развивающие технологии:
-использование Интернет-ресурсов и ресурсов электронных библиотек.
2. Развивающие проблемно-ориентированные технологии:
- проблемные лекции и семинары;
- «работа в команде» - совместная деятельность под руководством лидера, направленная на решение общей поставленной задачи;
- «междисциплинарное обучение» - использование знаний из разных областей, группируемых и концентрируемых в контексте конкретно решаемой задачи.
3. Личностно -ориентированные технологии обучения:
- консультации;
- «индивидуальное обучение» - выстраивание для студента собственной образовательной траектории с учетом интереса и предпочтения студента.
| № пп | Наименование темы дисциплины | Вид занятий (лекция, семинары, практические занятия) | Количество ак. ч. | Наименование активных и интерактивных форм проведения занятий |
| Базисы в гильбер-товом простран-стве. Разложение Фурье. | Лекция | Проблемная лекция | ||
| Линейные опера-торы в гильбер-товых простран-ствах. | Лекция | Проблемная лекция | ||
| Собственные зна-чения и собст-венные функции операторов.Спектр эрмитова (само-сопряженного) оператора | Практические занятия | Групповое обсуждение | ||
| Введение в аппа-рат обобщенных функций | Лекция | Проблемная лекция | ||
| Введение в аппа-рат обобщенных функций | Практические занятия | Групповое обсуждение |
12.2. Формы организации самостоятельной работы обучающихся (темы, выносимые для самостоятельного изучения; вопросы для самоконтроля; типовые задания для самопроверки
Date: 2015-09-18; view: 380; Нарушение авторских прав