Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Контрольная работа по курсу. «Введение в математический аппарат квантовой механики»
|
|
«Введение в математический аппарат квантовой механики»
Линейные, нормированные и гильбертовы пространства. Базисы в гильбертовых пространствах.
Вариант 1.
1. В пространстве со скалярным произведением докажите поляризационное тождество
,
где i – мнимая единица.
2. В комплексном гильбертовом пространстве функций, модуль которых квадратично интегрируем на отрезке [0,1], найти норму разности элементов х1(t) =(1+i)t и х2(t) = t2, где i – мнимая единица.
3. В гильбертовом пространстве вещественных квадратично интегрируемых на отрезке [-1;1] функций найдите норму разности элементов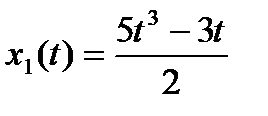 
и x2(t)= 
, нормы этих элементов и их скалярное произведение.
Контрольная работа по курсу
«Введение в математический аппарат квантовой механики»
Линейные, нормированные и гильбертовы пространства. Базисы в гильбертовых пространствах.
Вариант 2.
1. В комплексном гильбертовом пространстве функций, модуль которых квадратично интегрируем на отрезке [0,1 ], найти норму разности элементов х1(t) =(1+i)t и х2(t) = it2, где i – мнимая единица.
2.В пространстве со скалярным произведением выразите через скалярное произведение (y,x) – следующее выражение
,
где i – мнимая единица.
3. В гильбертовом пространстве вещественных квадратично интегрируемых на отрезке [-1;1] функций найти норму разности элементов x1(t)=t и x2(t)= ,нормы этих элементов и их скалярное произведение.
6.2.3. Контрольная работа №2
а) типовые задания (вопросы) - образец:
Date: 2015-09-18; view: 353; Нарушение авторских прав