
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Г. Обнинск 2015 г
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Национальный исследовательский ядерный университет «МИФИ»
Обнинский институт атомной энергетики –
филиал федерального государственного автономного образовательного учреждения высшего
профессионального образования «Национальный исследовательский ядерный университет «МИФИ»
(ИАТЭ НИЯУ МИФИ)
| УТВЕРЖДАЮ |
| И.о. декана физико-энергетического факультета ____________ А.В.Нахабов |
| «______»____________ 2015 г. |
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
Введение в математический аппарат квантовой механики
| название дисциплины |
| для студентов направления подготовки |
| 14.03.02 Ядерные физика и технологии |
| код и наименование направления подготовки |
| профиля |
| Ядерные реакторы и энергетические установки |
| код и наименование специализации/профиля(выбрать) |
| Форма обучения: очная |
г. Обнинск 2015 г.
Программа составлена в соответствии с федеральным государственным образовательным стандартом высшего образования по направлению подготовки 14.03.02 Ядерные физика и технологии.
Программу составил:
В.Л.Шаблов, профессор кафедры перспективных методов получения и преобразования энергии, д.ф.-м.н., проф.
Рецензент:
___________________ И.О. Фамилия, должность, ученая степень, ученое звание
Программа рассмотрена на заседании выпускающей кафедры перспективных методов получения и преобразования энергии
(протокол № ____ от «____»_____________2014 г.)
| Заведующий кафедрой перспективных методов получения и преобразования энергии ___________________ А.В.Зродников «____»_____________2014 г. |
1. Перечень планируемых результатов обучения по дисциплине, соотнесенных с планируемыми результатами освоения образовательной программы
В результате освоения ООП бакалавриата обучающийся должен овладеть следующими результатами обучения по дисциплине:
| Коды компетенций | Результаты освоения ООП Содержание компетенций | Перечень планируемых результатов обучения по дисциплине |
| ОПК-1 | способность использовать основные законы естест-веннонаучных дисциплин в профессиональной дея-тельности, применять ме-тоды математического анализа и моделирования, теоретического и экспе-риментального исследо-вания | Знать: математический аппарат квантовой механики, включая элементы функционального анализа (теория гильбертовых пространств, линейных операто-ров и элементы спектральной теории эрмитовых операторов) Уметь: использовать методы функционального анализа для описания квантовых систем Владеть: элементами теории гильбертовых пространств, линейных операторов и спект-ральной теории эрмитовых операторов |
2. Место дисциплины в структуре ООП бакалавриата
Дисциплина реализуется в рамках вариативной части. Индекс дисциплины: указать в соответствии с учебным планом.
Для освоения дисциплины необходимы компетенции, сформированные в рамках изучения следующих дисциплин: Физика I-III, Атомная физика, Математический анализ, Аналитическая геометрия, линейная алгебра, Векторный и тензорный анализ, Интегральные уравнения, Уравнения математической физики.
Дисциплины, для которых освоение данной дисциплины необходимо как предшествующее: Теоретическая физика, Взаимодействия частиц, Введение в квантовую теорию рассеяния и ее приложения к ядерной физике.
Дисциплина изучается на 3 курсе в 5 семестре.
3. Объем дисциплины в зачетных единицах с указанием количества академических часов, выделенных на контактную работу обучающихся с преподавателем (по видам занятий) и на самостоятельную работу обучающихся
| Вид работы | Форма обучения(вносятся данные по реализуемым формам) | |
| Очная | Заочная | |
| Семестр 5 | Курс 3 | |
| Количество часов на вид работы: | ||
| Контактная работа обучающихся с преподавателем | ||
| Аудиторные занятия (всего) | ||
| В том числе: | ||
| лекции (лекции в интерактивной форме) | (11) | |
| практические занятия (практические занятия в интерактивной форме) | (6) | |
| лабораторные занятия | ||
| Промежуточная аттестация | ||
| В том числе: | ||
| зачет | ||
| Самостоятельная работа обучающихся | ||
| Самостоятельная работа обучающихся (всего) | ||
| В том числе: | ||
| Проработка учебного (теоретического) материала | ||
| Подготовка ко всем видам контрольных испытаний текущего контроля успеваемости (в течение семестра) | ||
| Подготовка ко всем видам конт-рольных испытаний промежуточ-ной аттестации (по окончании семестра) | ||
| Всего (часы): | ||
| Всего (зачетные единицы): |
4. Содержание дисциплины, структурированное по темам (разделам) с указанием отведенного на них количества академических часов и видов учебных занятий
4.1. Разделы дисциплины и трудоемкость по видам учебных занятий (в академических часах)
| № п/п | Наименование раздела /темы дисциплины | Виды учебной работы в часах (данные по реализуемым формам) | |||||||||
| Очная форма обучения | Заочная форма обучения | ||||||||||
| Лек | Пр | Лаб | Внеауд | СРО | Лек | Пр | Лаб | Внеауд | СРО | ||
| 1. | Линейные (векторные)пространства | ||||||||||
| 1.1. | Линейные пространства. Нормированные пространства. | ||||||||||
| 1.2. | Пространства со скалярным произве-дением.Гильбертовы пространства. | ||||||||||
| 1.3 | Базисы в гильбертовом пространстве. Разложение Фурье. | ||||||||||
| 2. | Линейные функционалы и линейные операторы в гильбертовых пространствах | ||||||||||
| 2.1. | Линейные функционалы в гильбертовых пространствах. Теорема Рисса-Фреше | ||||||||||
| 2.2. | Линейные операторы в гильбертовых пространствах. | ||||||||||
| 2.3 | Собственные значения и собственные функции операторов. Спектр эрмитова (самосопряженного) оператора. | ||||||||||
| 2.4 | Введение в аппарат обобщенных функций | ||||||||||
| Всего: |
Прим.: Лек – лекции, Пр – практические занятия / семинары, Лаб – лабораторные занятия, Внеауд – внеаудиторная работа, СРО – самостоятельная работа обучающихся
4.2. Содержание дисциплины, структурированное по разделам (темам)
Лекционный курс
| № | Наименование раздела /темы дисциплины | Содержание |
| 1. | Линейные (векторные)пространства | |
| 1.1. | Линейные простран-ства. Нормированные пространства. | Линейные пространства. Нормированные прост-ранства.Сходимость элементов в нормированных пространствах. |
| 1.2. | Пространства со скалярным произве-дением.Гильбертовы пространства | Пространства со скалярным произведением. Свойства скалярного произведения. Пространство L2. Гильбертовы пространства. Теорема Фишера. |
| 1.3 | Базисы в гильбер-товом пространстве. Разложение Фурье. | Ортонормированные системы элементов в гиль-бертовом пространстве. Полнота ортонормирован-ной системы элементов. Базисы в гильбертовом пространстве. Разложение Фурье. Равенство Парсеваля. |
| 2. | Линейные функционалы и линейные операторы в гильбертовых пространствах | |
| 2.1. | Линейные функцио-налы в гильбертовых пространствах. | Линейные функционалы в гильбертовых пространствах. Теорема Рисса-Фреше |
| 2.2. | Линейные операторы в гильбертовых пространствах. | Линейные операторы в гильбертовых простран-ствах. Эрмитовы, унитарные, проекционные операторы. Функция от операторов. Операторы импульса, кинетической энергии, квантовомехани-ческий гамильтониан |
| 2.4 | Собственные значе-ния и собственные функции операторов. Спектр эрмитова (самосопряженного) оператора | Собственные значения и собственные функции операторов. Понятие спектра оператора. Дискрет-ный и непрерывный спектр. Спектр эрмитова (самосопряженного) оператора |
| 2.4 | Введение в аппарат обобщенных функций | Необходимость введения обобщенных функций. Пространство основных функций. Сингулярные и регулярные обобщенные функции. 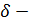 функция Дирака и ее свойства. Применения обобщенных функций. Обобщенные собственные значения и обобщенные собственные функции эрмитова (самосопряженного) оператора функция Дирака и ее свойства. Применения обобщенных функций. Обобщенные собственные значения и обобщенные собственные функции эрмитова (самосопряженного) оператора
|
Практические/семинарские занятия
| № | Наименование раздела /темы дисциплины | Содержание |
| 1. | Линейные (векторные)пространства | |
| 1.1. | Линейные простран-ства. Нормированные пространства. | Линейные пространства. Нормированные прост-ранства.Сходимость элементов в нормированных пространствах. |
| 1.2. | Пространства со скалярным произве-дением.Гильбертовы пространства | Пространства со скалярным произведением. Свойства скалярного произведения. Пространство L2. Гильбертовы пространства. |
| 1.3 | Базисы в гильбер-товом пространстве. Разложение Фурье. | Ортонормированные системы элементов в гиль-бертовом пространстве. Полнота ортонормирован-ной системы элементов. Базисы в гильбертовом пространстве. Разложение Фурье. Коэффициенты Фурье. Равенство Парсеваля. Классические орто-гональные полиномы, применяемые в квантовой механике (Эрмита, Лежандра, Лягерра) |
| 2. | Линейные функционалы и линейные операторы в гильбертовых пространствах | |
| 2.1. | Линейные функцио-налы в гильбертовых пространствах. | Линейные функционалы в гильбертовых пространствах. Теорема Рисса-Фреше. |
| 2.2. | Линейные операторы в гильбертовых пространствах. | Линейные операторы в гильбертовых пространствах. Норма оператора. Эрмитовы, унитарные, проекционные операторы. Функция от операторов. Операторы импульса, кинетической энергии, квантовомеханический гамильтониан. |
| 2.3 | Собственные значе-ния и собственные функции операторов. Спектр эрмитова (самосопряженного) оператора | Собственные значения и собственные функции операторов. Понятие спектра оператора. Дискрет-ный и непрерывный спектр. Спектр эрмитова (самосопряженного) оператора. |
| 2.4 | Введение в аппарат обобщенных функций | Пространство основных функций. Сингулярные и регулярные обобщенные функции.  функция Дирака и ее свойства. Применения обобщенных функций. функция Дирака и ее свойства. Применения обобщенных функций.
|
5. Перечень учебно-методического обеспечения для самостоятельной работы обучающихся по дисциплине
1. Электронный учебно-методический комплекс дисциплины «Введение в математический аппарат квантовой механики» – http://iate.obninsk.ru/node/5230
6. Фонд оценочных средств для проведения промежуточной аттестации обучающихся по дисциплине
6.1. Паспорт фонда оценочных средств по дисциплине
| № п/п | Контролируемые разделы (темы) дисциплины (результаты по разделам) | Код контролируемой компетенции (или её части) / и ее формулировка | Наименование оценочного средства |
| Текущий контроль, 1 семестр | |||
| 1. | Линейные пространства. Нормированные прост-ранства. Пространства со скалярным произведени-ем. Гильбертовы прост-ранства.Базисы в гильбер-товых пространствах пространства. Разложение Фурье. | ОПК-1 способность использовать основные законы естественно-научных дисциплин в профессиональной дея-тельности, применять методы математичес-кого анализа и модели-рования, теоретичес-кого и эксперименталь-ного исследования Знать: математический аппарат квантовой механики, включая элементы функцио-нального анализа (теория гильбертовых пространств, линейных операторов и элементы спектральной теории эрмитовых операторов) | Контрольная работа №1 |
| 2. | Линейные операторы в гильбертовых простран-ствах. Собственные значения и собственные функции операторов. Спектр эрмитова (само-сопряженного) оператора. | ОПК-1 способность использовать основные законы естественно-научных дисциплин в профессиональной дея-тельности, применять методы математичес-кого анализа и модели-рования, теоретичес-кого и эксперименталь-ного исследования. Знать: математический аппарат квантовой механики, включая элементы функцио-нального анализа (теория гильбертовых пространств, линейных операторов и элементы спектральной теории эрмитовых операторов) Владеть: элементами теории гильбертовых пространств, линейных операторов и спект-ральной теории эрми-товых операторов. | Контрольная работа №2 |
| Промежуточный контроль, 1 семестр | |||
| Зачет | Вопросы к зачету | ||
| Всего: |
6.2. Типовые контрольные задания или иные материалы, необходимые для оценки знаний, умений, навыков и (или) опыта деятельности, характеризующие этапы формирования компетенций в процессе освоения образовательной программы
6.2.1. Зачет
а) типовые вопросы (задания):
1.Линейные (векторные) пространства. Линейная зависимость и линейная независимость элементов. Базисы в линейных пространствах.
2.Нормированные пространства. Аксиомы нормы.
3.Векторные пространства с внутренним (скалярным) произведением (предгильбертовы пространства). Свойства скалярного произведения.
4.Полные нормированные пространства. Гильбертовы пространства.
5. Ортогональные системы элементов в гильбертовых пространствах. Базисы в гильбертовых пространствах. Разложение Фурье. Коэффициенты Фурье. Равенство Парсеваля. Применение разложения Фурье в квантовой механике. Полиномы Эрмита, Лежандра, Лягерра. Коэффициенты Фурье как амплитуды вероятности.
6.Пространство L2 и его свойства. Теорема Фишера о полноте пространства L2. Пространство L2 в квантовой механике.
7.Линейные функционалы. Теорема Рисса-Фреше об ограниченном линейном функционале.
8.Обобщенные функции. Пространство основных функций. Сингулярные и регуляр- ные обобщенные функции. Действия над обобщенными функциями. Производная обобщенной функции.  функция Дирака и ее свойства. Применения обобщенных функций.
функция Дирака и ее свойства. Применения обобщенных функций.
9.Линейные операторы в гильбертовых пространствах. Непрерывные и ограниченные
операторы. Норма оператора.
10.Сопряженные операторы. Эрмитовы опнраторы. Самосопряженные операторы.
11.Унитарные и проекционные операторы. Функции от операторов. Унитарная экспонента.
12.Линейные операторы в квантовой механике. Операторы импульса, кинетической энергии, Шредингера.
13.Собственные значения и собственные функции эрмитова (самосопряженного) оператора. Обобщенные собственные значения и обобщенные собственные функции. Спектр оператора. Резольвента.
14.Элементы спектральной теории самосопряженных операторов.
критерии оценивания компетенций (результатов):
Оценка «отлично» - за глубокие знания учебного материала, содержащегося в основных и дополнительных рекомендуемых литературных источниках, умение четко и безошибочно (практически безошибочно) анализировать явления и проблемы; логично и последовательно отвечать на поставленные вопросы, умение применять теоретические положения при решении практических задач. Оценка «хорошо» - за прочные знания учебного материала; аргументированные ответы на поставленные вопросы, которые, однако, содержат определенные (несущественные) неточности, умение применять теоретические положения при решении практических задач. Оценка «удовлетворительно» - за посредственные знания учебного материала, слабо аргументированные ответы, слабое применение теоретических положений при решении практических задач. Оценка «неудовлетворительно» - за незнание значительной части учебного материала, существенные ошибки в ответах на вопросы, неумение ориентиро-ваться при решении практических задач, незнание основных фундаментальных положений изучаемой дисциплины.
описание шкалы оценивания:
Оценка «отлично»- 90-100 баллов
Оценка «хорошо»- 75-89 баллов
Оценка «удовлетворительно»- 60-74 баллов
Оценка «неудовлетворительно»- меньше 59 баллов
6.2.2.Контрольная работа №1
а) типовые задания (вопросы) - образец:
Date: 2015-09-18; view: 374; Нарушение авторских прав