Уравнение состояния идеального газа

Понятие идеального газа.

Идеальным называется газ, у которого объемы молекул бесконечно малы и отсутствуют силы молекулярного взаимодействия. Молекулы идеального газа представляют собой материальные точки, взаимодействие между которыми ограничено молекулярными соударениями.

Любой реальный газ тем ближе к идеальному, чем ниже его давление и выше температура. Например, окружающий нас воздух можно считать идеальным газом. Понятие идеального газа и законы идеальных газов полезны в качестве предела законов реального газа.

На практике часто приходится иметь дело с газами при невысоких давлениях, поэтому расчеты различных термодинамических процессов с достаточной степенью точности можно проводить по уравнениям идеального газа.

Уравнение состояния идеального газа.

Из уравнени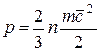й , и 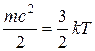, следует, что .

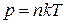Рассмотрим 1 кг газа. Учитывая, что в нем содержится N молекул и, следова­тельно, , получим: .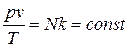

Постоянную величину Nk, отнесен­ную к 1 кг газа, обозначают буквой R и называют газовой постоян­ной. Поэтому

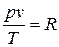, или 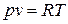. (1.3)

Полученное соотношение представляет собой уравнение Клапейрона.

Умножив (1.3) на М, получим урав­нение состояния для произвольной массы газа М:

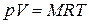. (1.4)

Уравнению Клапейрона можно при­дать универсальную форму, если отнести газовую постоянную к 1 кмолю газа, т. е. к количеству газа, масса которого в килограммах численно равна молеку­лярной массе μ. Положив в (1.4) М= μ и V=V μ, получим для одного моля урав­нение Клапейрона — Менделеева:

.

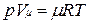Здесь 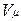— объем киломоля газа, а 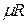— универсальная газовая постоянная.

В соответствии с законом Авогадро (1811г.) объем 1 кмоля, одинаковый в одних и тех же условиях для всех иде­альных газов, при нормальных физических условиях равен 22,4136 м³, поэтому

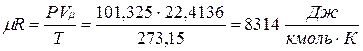
Газовая постоянная 1 кг газа составляет .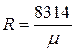

Date: 2015-09-18; view: 452; Нарушение авторских прав