Оболочечная модель ядра

Оболочечная модель ядра рассматривает ядро как систему нуклонов, движущихся независимо в потенциальном поле, создаваемом другими нуклонами. Эта модель относится к моделям второй группы. Она возникла в начале 1930 годов по аналогии с моделью электронных оболочек атома. Предположения лежащие в основе оболочечной модели 1.Сферическая симметрия среднего потенциала ядра. 2.Отсутствие взаимодействия между нуклонами. 3.Обобщенный принципа Паули для нуклонов: волновая функция фермионов, зависящих от спиновых, пространственных и изоспиновых координат, должна быть антисимметрична при перестановке двух нуклонов.

Простейшим вариантом оболочечной модели является одночастичная модель ядра. для ядра с нечетным числом нуклонов. Все нуклоны образуют сферически симметричный остов с нулевыми механическими и магнитными моментами, а свойства ядра определяются последним нечетным нуклоном. Уравнение Шредингера имеет вид

Hψ = 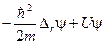= Eψ (1.16)

где U = V(r) +U_SL,

V(r) -потенциал Саксона- Вудса, U_SL = U(r) (s, l) – спин-орбитальный потенциал.

Волновая функция ядра представляется в виде произведения волновых функций – решений уравнения Шредингера для одного нуклона, движущегося в центральном поле с потенциалом Саксона- Вудса. В ядрах, как правило, осуществляется сильная j- j связь: орбитальный момент l и спин s векторно складываются в полный угловой момент нуклона j= l+ s, а векторы моментов отдельных нуклонов складываются в полный угловой момент ядра I.

Состояние нуклона в сферическом ядре полностью характеризуется четырьмя квантовыми числами (n,l,j,m).

Главное квантовое число n =1,2,3,... нумерует уровни энергии Е,

орбитальное квантовое число l =0,1,2,3,… n -1 нумерует орбитальный момент l,

квантовое число j = l 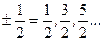нумерует полный угловой момент нуклона j,

квантовое число 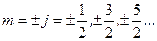(всего 2j+1 значение) нумерует проекцию полного углового момента на ось квантования.

Согласно одночастичной модели ядра нуклоны данного сорта (протоны и нейтроны) заполняют j - уровень (свою подоболочку) согласно принципу минимума энергии и принципу Паули (в каждом квантовом состоянии один нуклон).

Термы нуклонов обозначаются .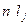

Пример: На уровне энергии с n = 1 в состоянии s квантовое число l =0, число нуклонов N = 2(2l+1) = 2, терм 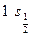. На уровне n =1 в состоянии р, l =1, j =1/2, 3/2 N=2(2+3) = 6 нуклонов, термы 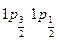. см рис. 1.4

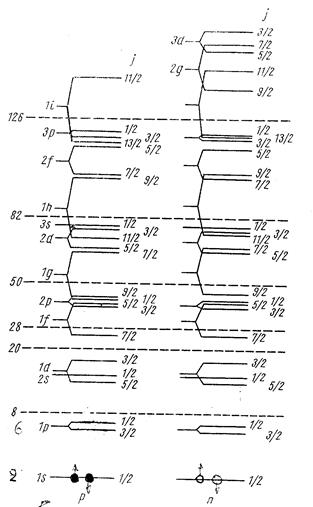
Рис.1.4 Структура ядерных уровней для протонной и нейтронных подсистем ядра.

Одночастичная модель ядра объясняет повышенную устойчивость магических ядер с числом нейтронов N и протонов Z равных 2; 8; 20; 28; 50 и N =126 как следствие полного заполнения нуклонами своих подоболочек.

Одночастичная модель правильно описывает спины и магнитые моменты нечетных ядер. Магнитный момент нечетного ядра μ определяется только последним нуклоном.

Пример: для нейтронно-нечетного ядра (число протонов четное) магнитный момент:

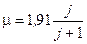μ_B при j = l – 1/2,

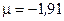μ_В при j = l +1/2. (1.17)

Date: 2015-09-05; view: 711; Нарушение авторских прав