Одномерное движение частицы

Одним из важных приложений закона сохранения механической энергии является вопрос о границах движения частицы в поле потенциальных сил. Допустим, что непотенциальные силы в системе не действуют. Тогда справедлив закон сохранения механической энергии. Поскольку кинетическая энергия по своему смыслу не может быть меньше нуля, то из закона сохранения механической энергии следует, что

.

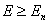Этим соотношением определяется область изменения всех координат системы, в которой частица может находиться при заданной энергии Е. В область, где 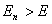, частица попасть не может, так как потенциальная энергия не может превышать полную.

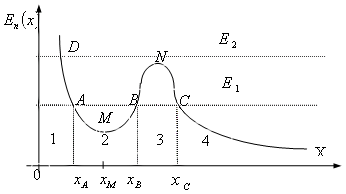Рис. 3.12. Одномерное движение частицы

Рассмотрим одномерное движение частицы. Примем направление движения частицы за координатную ось X, следовательно, потенциальная энергия будет зависеть только от координаты x:

.

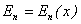Если Е – полная механическая энергия, то частица может находиться только в тех местах оси X, где .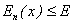

Допустим, что график 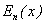имеет вид, изображенный на рис. 3.12. Проведем на этом рисунке горизонтальную прямую 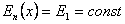. Пусть эта горизонтальная прямая пересекает кривую 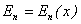в трех точках А, В, С с координатами 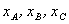. Очевидно, частица с полной энергией 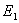не может находиться в областях 1 и 3. Она может двигаться либо в области 2, либо в области 4. Переходить из области 2 в область 4 или обратно частица не может. Область, в которой не может находиться частица и для преодоления которой требуется дополнительный запас энергии, называется потенциальным барьером. Переходу из области 2 в область 4 и обратно препятствует «потенциальный барьер» BNC.

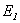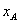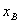В области 2 частица с полной энергией будет совершать так называемое финитное движение, то есть движение, происходящее в ограниченной области пространства. В точках и потенциальная энергия равна полной энергии, поэтому в этих точках кинетическая энергия, а с ней и скорость частицы, равна нулю. В точке 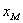потенциальная энергия минимальна, а кинетическая энергия и скорость имеют максимальное значение. 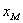Так как сила связана с потенциальной энергией соотношением , то между точками и 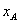она будет положительной, а между точкам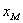и и 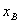– отрицательной. Это значит, что между точкам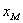и и 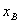сила направлена в сторону уменьшения x, то есть налево, а между точкам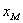и и 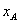– направо. Поэтому, если частица начинает двигаться от точки 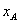, где ее скорость равна нулю, то под действием силы, направленной вправо, она будет постепенно ускоряться и достигнет в точке 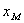максимальной скорости. Двигаясь далее от 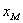до 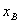под действием силы, направленной теперь влево, частица будет замедляться, пока ее скорость в точке 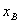не станет равной нулю. После этого она начинает обратное движение от точки 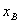к точке 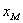. Такое движение будет повторяться все время. Частица будет колебаться в указанной области, называемой потенциальной ямой.

Если же частица находится в области 4 и движется влево, то она, достигнув точки 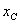, повернет обратно и далее будет уходить на бесконечность. Такое движение называется инфинитным.

Пусть теперь частица обладает большей энергией 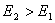, и горизонтальная прямая 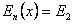пересекает потенциальную кривую в единственной точке D с абсциссой . Тогда для частицы окажется доступной вся область пространства правее точки и движение в этой области будет инфинитным.

В точке 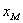потенциальная энергия достигает минимума. Это положение является положением устойчивого равновесия, так как при отклонении частицы от положения равновесия в рассматриваемом случае возникает сила, стремящаяся вернуть частицу назад в положение равновесия. Если частица находится в положении, соответствующем максимуму потенциальной энергии, то при отклонении частицы в том или ином направлении из точки максимума потенциальной энергии возникает сила, в обоих случаях действующая в сторону удаления от этой точки. Поэтому места, где потенциальная энергия достигает максимума, являются положениями неустойчивого равновесия.

Date: 2015-09-17; view: 358; Нарушение авторских прав