Описание движения

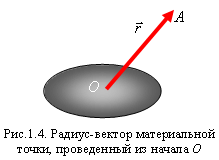
Радиус-вектор. В выбранной системе отсчёта положение материальной точки А, которую в дальнейшем будем называть частицей, можно задать вектором 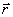, проведенным из некоторой неподвижной точки О выбранного тела отсчета в точку А (рис. 1.4). Этот вектор называется радиус-вектором. 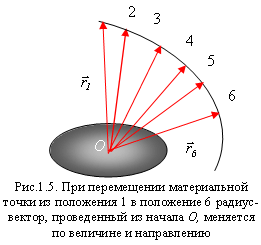При движении частицы ее радиус-вектор меняется в общем случае как по модулю, так и по направлению, то есть радиус-вектор зависит от времени 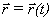(рис. 1.5).

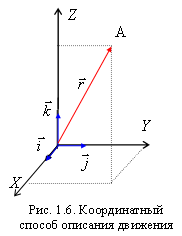
Положение любой точки в декартовой системе координат может быть охарактеризовано координатами 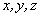(рис. 1.6). При этом радиус-вектор точки тоже может быть выражен через ее координаты.

,

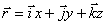где 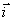, , 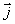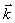– координатные орты, то есть векторы, направленные вдоль координатных осей и по модулю равные единице, 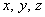– проекции радиус-вектора на оси системы координат.

Траектория. Конец радиус-вектора с течением времени перемещается вместе с частицей. Вычерчиваемая им при этом воображаемая линия называется траекторией движения частицы. Она может быть видимой или невидимой. Например, траектория движения автомобиля по автостраде не видна, а след, оставляемый реактивным самолетом в голубом небе (рис. 1.7), зигзаг молнии на фоне тучи (рис. 1.8) являются видимыми траекториями движения.

По виду траектории движения разделяют на прямолинейные и криволинейные. Например, траектория движения пули от пистолета до мишени – отрезок прямой линии; траектория самолета, выполняющего «мертвую петлю» – окружность.

Траектории небесных тел называются орбитами. Орбиты планет Солнечной системы и некоторых комет являются эллипсами. Существуют кометы, орбиты движения которых являются параболами.

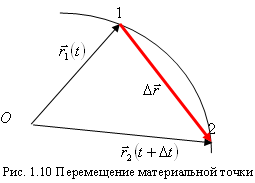
Перемещение. Путь. Пусть за промежуток времени точка А переместилась из положения 1 в положение 2. Обозначим радиус-вектор начального положения точки А через 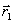, а радиус-вектор конечного положения – через .

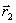Вектор 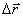, проведенный из начального положения частицы в конечное, называется вектором перемещения (рис. 1.10).

.

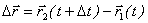Вектор перемещения равен разности радиус-векторов конечного и начального положения частицы. Вектор перемещения также может быть выражен через его проекции на оси декартовой системы координат:

.

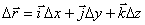Здесь 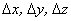являются проекциями вектора перемещения на оси декартовой системы координат.

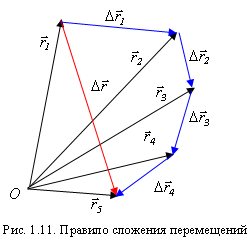
Если частица последовательно совершает несколько перемещений 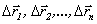, то полное перемещение равно векторной сумме отдельных перемещений 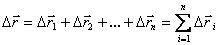(рис. 1.11).

Длина участка траектории между начальным и конечным положениями материальной точки называется путем или расстоянием, пройденным точкой.

Средняя скорость. Быстроту, с которой совершается перемещение, можно охарактеризовать средней скоростью. Если за промежуток времени совершается перемещение 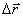, то отношение 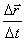называется средней скоростью частицы за время :

.

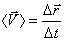Вектор средней скорости совпадает по направлению с вектором перемещения.

Средняя скорость относится к определенному промежутку времени, поэтому для одного и того же движения она может быть различной для различных промежутков времени. Если при своем движении частица возвращается в исходное положение, то ее перемещение, а следовательно, и средняя скорость, равны нулю, тогда как на любом участке траектории это не так. Обращение в нуль средней скорости при движении по замкнутой траектории связано с ее векторным характером.

Иногда необходимо знать путь, проходимый за какое-то определенное время. В этом случае наряду со средней скоростью по перемещению целесообразно ввести среднюю скорость прохождения пути. Если за промежуток времени частица проходит путь 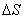, то средняя скорость прохождения пути равна

.

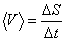Средняя скорость прохождения пути – величина скалярная. Когда говорят о скорости движения поездов, судов, пешеходов, то обычно имеют в виду именно эту скорость.

Заметим, что в общем случае 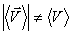. Равенство имеет место только при прямолинейном движении в одном направлении. Зная среднюю скорость прохождения пути, можно приближенно вычислить путь, пройденный за определенное время или время прохождения определенного пути.

Мгновенная скорость. До сих пор мы характеризовали движение только средней скоростью, которая равна отношению перемещения ко времени. Чтобы исследовать закономерности движения и управлять движением какого-либо тела, необходимо знать скорость его движения в каждой точке траектории, или, что то же самое, в каждый момент времени. Такая скорость называется мгновенной. Особенно важно уметь определять мгновенную скорость движения тела, когда скорость движения меняется как по модулю, так и по направлению.

Для определения мгновенной скорости движения тела в некоторой точке нужно измерить перемещение за такой малый промежуток времени , за который можно считать скорость практически неизменной. Поэтому можно дать такое определение мгновенной скорости: мгновенная скорость равна отношению очень малого перемещения к промежутку времени, за которое оно совершилось:

.

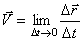Обозначение lim следует читать как предел. (Слово «предел» образовано от латинских слов "limes" и "limitis" – граница, предел.) В математике величину такого предела называют производной функции 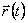по времени. Для нее в математике используется обозначение

.

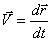Здесь под 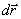понимается бесконечно малое перемещение, которое частица совершает за бесконечно малый промежуток времени .

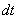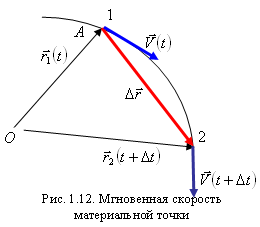
Таким образом, мгновенная скорость равна производной от радиус-вектора по времени. Направление мгновенной скорости совпадает с направлением малого перемещения в данной точке. В случае прямолинейного движения вектор мгновенной скорости совпадает с траекторией движения. В случае криволинейного движения при уменьшении промежутка времени вектор перемещения будет поворачиваться вокруг точки 1 и в пределе займет положение касательной к траектории в точке 1 (рис. 1.12). Таким образом, мгновенная скорость равна производной от радиус-вектора по времени и направлена по касательной к траектории в данной точке в сторону движения, то есть мгновенная скорость характеризует быстроту изменения радиус-вектора со временем. Модуль мгновенной скорости .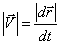

Так как изменения координат 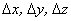являются проекциями вектора перемещения 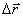на соответствующие оси координат, то скорости изменения координат определятся следующим образом:

, , ,

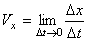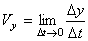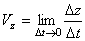или

, , .

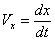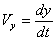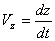Таким образом, проекции вектора скорости на оси декартовой системы координат являются производными соответствующих координат по времени.

Вектор мгновенной скорости можно, как любой вектор, записать через его проекции на оси :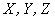

,

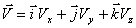или

.

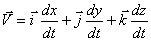Модуль векто ра скорости определяется через его проекции по общему для всех векторов правилу:

.

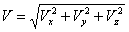Ускорение. При движении тел их скорости могут меняться как по величине, так и по направлению. Величину, характеризующую быстроту изменения скорости, называют ускорением. Ускорение равно пределу отношения изменения скорости 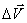к промежутку времени , в течение которого это изменение произошло:

,

следовательно, ускорение – это производная скорости по времени:

.

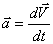Ускорение – важнейшая физическая величина, потому что, как будет видно в дальнейшем, действия одних тел на другие определяют не скорости тел, а ускорения.

В отличие от вектора скорости, который всегда направлен по касательной к траектории, вектор ускорения может иметь составляющие, направленные как по касательной, так и по нормали к траектории.

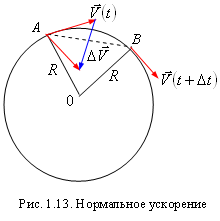
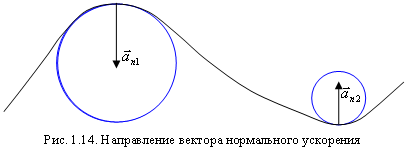
Нормальное ускорение. Рассмотрим частный случай движения точки по криволинейной траектории – движение точки по окружности радиуса R с постоянной по модулю скоростью. В этом случае скорость постоянна по величине, но изменяется по направлению. Ускорение, которое характеризует изменение скорости по направлению, называют нормальным ускорением.

Можно показать, что вектор нормального ускорения в каждой точке траектории направлен к центру окружности, поэтому его называют еще центростремительным ускорением. Модуль нормального ускорения зависит от модуля вектора скорости и от радиуса окружности R. Получим эту зависимость.

Пусть частица перемещается из точки А в точку В за время D t (рис. 1.13). Радиусы ОА и ОВ перпендикулярны векторам скорост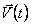и и 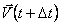. Перенесем вектор 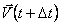параллельно самому себе в точку А. Тогда вектор приращения скорости 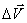будет замыкать треугольник, образованный этими скоростями. Из подобия равнобедренного треугольника, построенного на векторах скорост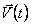и и 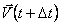, и треугольника АОВ следует:

.

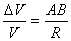При 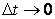длина хорды АВ будет стремиться к длине дуги 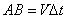, поэтому модуль нормального ускорения определится следующим соотношением:

.

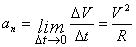При 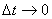вектор 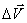поворачивается и в пределе будет направлен по радиусу к центру окружности, а, следовательно, и вектор нормального ускорения будет также направлен по радиусу к центру окружности.

Последнее выражение для нормального ускорения справедливо для определения нормального ускорения при движении точки по любой криволинейной траектории, так как достаточно малый участок траектории можно рассматривать как дугу некоторой окружности, совпадающей с траекторией на этом малом участке. Положение центра этой окружности и ее радиус будут своими для каждой точки траектории и, следовательно, изменяются от точки к точке. Вектор нормального ускорения в каждой точке траектории направлен к центру соответствующей окружности, то есть перпендикулярно к касательной к траектории (рис. 1.14).

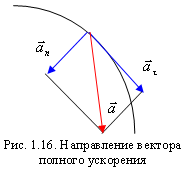
Тангенциальное ускорение. В общем случае неравномерного движения скорость может изменяться и по величине, и по направлению, поэтому изменение вектора скорости 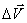за время D t можно представить как сумму 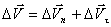(рис. 1.15). Поделив это выражение на D t и перейдя к пределу, получим:

,

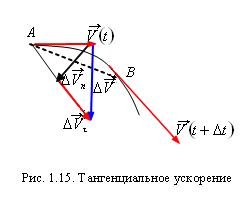
где 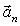– нормальное ускорение, 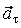– тангенциальное ускорение. Таким образом, тангенциальное ускорение характеризует изменение скорости по величине. При 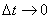точка В будет приближаться к точке А, а вектор 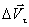стремится занять положение касательной к траектории. Следовательно, тангенциальное ускорение направлено по касательной к траектории, а его модуль .

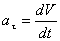Таким образом, тангенциальное ускорение указывает, насколько быстро изменяется скорость частицы по модулю. Нормальное ускорение указывает, насколько быстро скорость частицы изменяется по направлению. Направление вектора ускорения в случае криволинейного движения не совпадает с направлением вектора скорости (рис. 1.16). Модуль полного ускорения .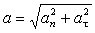

Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь, перемещение, скорость и ускорение. Путь является скалярной величиной. Перемещение, скорость и ускорение – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т.д.

Date: 2015-09-17; view: 534; Нарушение авторских прав