Теорема о замене переменных в неопределенном интеграле

Теорема об общем виде первообразной функции.

Т Пусть 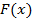– первообразная 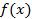на 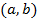. Тогда любая первообразная

функции 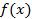на 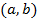имеет вид: 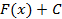, где 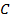– постоянная.

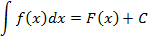
Доказательство:

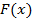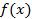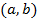Если – первообразная функции на и 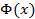– некоторая другая первообразная, то, по определению первообразно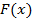й, и 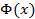дифференцируемы на 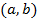и 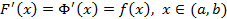, т.е. .

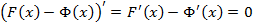Тогда, по критерию постоянства функци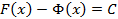и или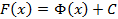

Свойства неопределенного интеграла (о взаимообратности операций интегрирования и дифференцирования, свойство линейности операции интегрирования).

1. Если функция 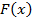дифференцируема на некотором промежутке, то на нем

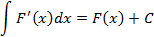
Доказательство:

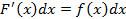
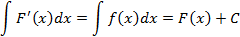
2. Пусть 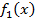и 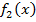имеют первообразные на некотором интервале,

тогда на этом промежутке имеют первообразные следующие функции,

а именно 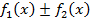, , 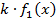где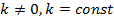

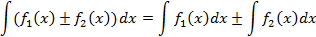
Доказательство:

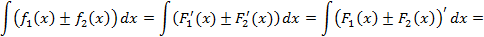
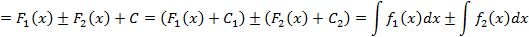
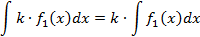
Доказательство:

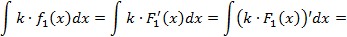
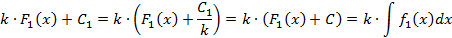
Теорема о замене переменных в неопределенном интеграле.

Т Пусть функци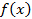и и 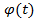определены на промежутках 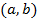и 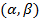соответственно, причем 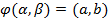, т. е. все значения функции 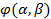принадлежат .

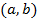Если функция 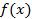имеет на 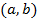первообразную 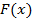, а функция 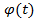дифференцируема на 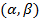, то следующая функция 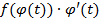имеет на 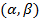первообразную 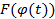и при этом выполняется равенство:

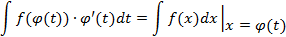
Доказательство:

Т.к. все значения ,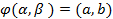

то на 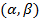определены сложные функци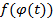и и .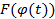

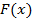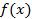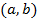Далее, т.к. - первообразная функции на , то , .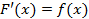

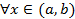Учитывая, что по условию функция 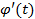также дифференцируема на .

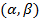Тогда по теореме о дифференцируемости сложной функции

можно найти производную от функции:

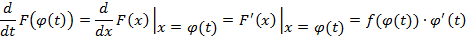
Последнее означает, что: 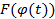является

первообразной функции 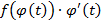на .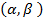

Таким образом,

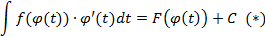
С другой стороны, по теореме об общем виде первообразной:

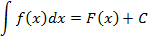
Подставим в него вместо :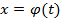

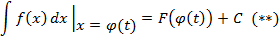
Учитывая, что 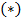и 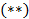равны правые части, то левые части тоже равны:

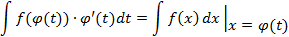
Замечание 1.

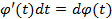
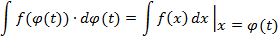
На этой формуле основан метод занесения под знак дифференциала.

Замечание 2.

Если функция 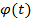имеет обратную функцию 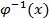, то:

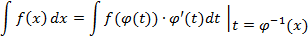
На этой формуле основан метод подстановки или замены переменной.

Date: 2015-09-05; view: 11906; Нарушение авторских прав