
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение ошибки репрезентативности (m)
|
|
Ошибка репрезентативности (m) показывает, насколько результаты полученные при выборочном исследовании, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования (генеральная совокупность).
Взаимосвязь объёма выборки и репрезентативности
· Репрезентативность не зависит от объема выборки. Репрезентативность достигается только тогда, когда в выборку отобраны объекты из разных групп, при условии, что их доли в генеральной и выборочной совокупности равны. Репрезентативность выборки зависит только от методики отбора единиц из генеральной совокупности в выборочную совокупность и не зависит от объема. Конечно, чем больше объем выборки, тем выше ее точность, однако, неверно распределенная выборка в 5000 единиц намного хуже, чем хорошо распределенная выборка в 500 единиц.
· Чем более однородна генеральная совокупность, тем меньший объем выборочной совокупности потребуется для получения точных результатов. Если, например, в генеральной совокупности все респонденты имеют одинаковый доход, то будет достаточно опросить одного респондента, чтобы узнать средний доход по совокупности. Чтобы определить вкус каши достаточно съесть одну ложку, а не всю тарелку, конечно, при условии, что каша хорошо перемешана.
При правильно составленной выборочной совокупности можно получить достаточно полное представление о закономерностях, присущих всей генеральной совокупности. Основным правилом составления выборочной совокупности является обеспечение ее репрезентативности, т.е. соответствия данных выборочной и генеральной совокупностей.
Выборочная совокупность должна быть представительной или репрезентативной (способность быть отражением генеральной совокупности), для чего необходимы следующие требования:
· обладать характерными чертами генеральной совокупности, т.е. по составу быть максимально похожей на неё;
· достаточной по объему, т.е. по числу наблюдений.
Формула ошибки репрезентативности (m) для относительных величин:
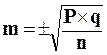 или
или 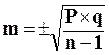 , если число наблюдений менее 30 случаев,
, если число наблюдений менее 30 случаев,
где:
Р – величина показателя;
q =100–P, если показатель рассчитан на 100;
q =1000 –P, если показатель вычислен на 1000, и т.д.;
n – число наблюдений.
Например: работающих на предприятии – 1400 человек (n), имеющих гипертоническую болезнь (ГБ) – 44 человека.
Показатель заболеваемости ГБ
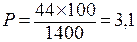 на 100 работающих, далее вычисляем по формуле
на 100 работающих, далее вычисляем по формуле
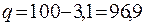
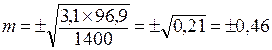 .
.
Вывод: результаты выборочной совокупности по определению ГБ на предприятии отличаются от генеральной совокупности на ± 0,46 (средняя ошибка ± 0,46).
Формула (m) для средней величины: 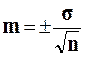 или
или 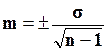 , если число наблюдений меньше 30.
, если число наблюдений меньше 30.
Например, у 49 больных (n) гастритом уровень пепсина М =1,0 г%, σ = ±0,35 г%
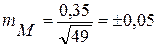 г%
г%
Вывод: результаты выборочной совокупности по определению уровня пепсина у 49 больных гастритом отличаются от генеральной совокупности (если бы исследования проводились у всех больных гастритом) на ± 0,05 (средняя ошибка ± 0,05).
Примечание: среднее квадратическое отклонение (σ) характеризует степень рассеивания вариант вокруг средней арифметической (смотри тему №3). Вычисляют по формуле: 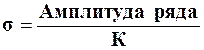
Амплитуда ряда (см. тему №4)
К – «коэффициент К», (см. приложение №3).
Доверительные границы (М, P) средних и относительных величин – это границы относительных или средних величин размеров признака выход за пределы которых, вследствие случайных колебаний, имеет незначительную вероятность.
Доверительные границы для средней величины по формуле:
Мген.=Мвыб.± tm, где:
Мген., выб . – доверительные границы средней величины генеральной и выборочной совокупности,
t – доверительный критерий (устанавливается исследователем, но должен быть не меньше 2, смотри ниже),
m – ошибка репрезентативности.
Доверительные границы для относительной величины по формуле:
Pген.=Pвыб.± tm, где:
Pген.,выб. – доверительные границы относительной величины генеральной и выборочной совокупности;
t – доверительный критерий (устанавливается исследователем, но должен быть не меньше 2, смотри ниже);
m – ошибка репрезентативности.
Предельная ошибка (Δ - дельта) – это максимальная средняя ошибка показателя (m) вычисляется по формуле:
Δ = tm ( максимально возможная погрешность оценки генеральной совокупности ),
где:
t – доверительный критерий (устанавливается исследователем, но должен быть не меньше 2, смотри ниже);
m – ошибка репрезентативности.
Вероятность безошибочного прогноза (p) – это вероятность, с которой можно утверждать, что в генеральной совокупности относительных или средних величин (P, M) показатели будут находиться в пределах ±tm. Для медицинских исследований степень вероятности безошибочного прогноза (p) должна быть не менее 95%, т.е отображать объективную реальность проведенных исследований на 95%, тогда t=2 (см. ниже).
Зависимость доверительного критерия от степени вероятности безошибочного прогноза p (при n>30)
Таблица 5.1
| Степень вероятности (p) | Доверительный критерий (t) |
| 95,0% | |
| 99,0% | |
| <95% |
Например, определить доверительные границы среднего уровня пепсина при М =1,0 г% у 49 больных гастритом при вероятности безошибочного прогноза равному 95%
n =49, p =95% (t=2), М =1,0г%, m =±0,05%
Доверительные границы Мген.= Мвыб.± tm, отсюда Мген =1+2×0,05
 не более 1 г% + 0,1% = 1,1 г%
не более 1 г% + 0,1% = 1,1 г%
 М
М
не менее 1 г% – 0,1 г% = 0,9%
Вывод: Установлено с вероятностью безошибочного прогноза 95% средний уровень пепсина в генеральной совокупности у больных гастритом не превышает 1,1 г% и не ниже 0,9 г%.
При сопоставлении двух сравниваемых величин необходимо не только определить их разность, но и оценить достоверность, т.е. достоверно или случайно их различие.
Date: 2015-09-17; view: 9707; Нарушение авторских прав