Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Кодирование линейных команд
|
|
Пример 1.
Оба операнда находятся в регистрах общего назначения: (AX)=a; (CX)=b. Для обращения к операндам используется прямая регистровая адресация.
Символическая запись команды:
ADD AX,CXСогласно табл. 6.2 машинное представление этой команды имеет вид:
000000dw md reg r/mПо условию операнды занимают полноразрядные регистры длиной 1 слово, следовательно, необходимо установить w=1.
Так как оба операнда располагаются в регистрах общего назначения, то любой из них можно закодировать в поле reg. Поэтому команда может иметь два различных представления в машинном коде. При этом, если в поле reg закодирован номер регистраAX, то бит приемника результата d=1. Если в поле reg закодирован номер регистра CX, то бит приемника результата d=0.
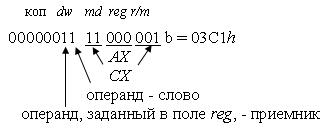
или
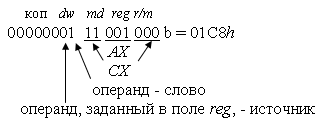
Здесь и далее в записи команд b означает двоичное представление, h - 16-е.
После выполнения команды в AX будет записана сумма содержимого регистров AX и CX, а указатель команды IP увеличится на длину выполненной команды (2 байта) и будет указывать на первый байт следующей команды.
Здесь и далее представление информации будем давать в 16-м виде, если другое не оговорено особо.
Если перед началом выполнения команды (AX)=0C34, (CX)=1020, (IP)=0012, то после ее выполнения (AX)=1C54,(CX)=1020, (IP)=0014.
Вопрос 2
Первое поколение ЭВМ (1948 — 1958 гг.)
Элементной базой машин этого поколения были электронные лампы – диоды и триоды. Машины предназначались для решения сравнительно несложных научно-технических задач. К этому поколению ЭВМ можно отнести: МЭСМ, БЭСМ-1, М-1, М-2, М-З, “Стрела”, “Минск-1”, “Урал-1”, “Урал-2”, “Урал-3”, M-20, "Сетунь", БЭСМ-2, "Раздан". Они были значительных размеров, потребляли большую мощность, имели невысокую надежность работы и слабое программное обеспечение. Быстродействие их не превышало 2—3 тысяч операций в секунду, емкость оперативной памяти—2К или 2048 машинных слов (1K=1024) длиной 48 двоичных знаков. В 1958 г. появилась машина M-20 с памятью 4К и быстродействием около 20 тысяч операций в секунду. В машинах первого поколения были реализованы основные логические принципы построения электронно-вычислительных машин и концепции Джона фон Неймана, касающиеся работы ЭВМ по вводимой в память программе и исходным данным (числам). Этот период явился началом коммерческого применения электронных вычислительных машин для обработки данных. В вычислительных машинах этого времени использовались электровакуумные лампы и внешняя память на магнитном барабане. Они были опутаны проводами и имели время доступа 1х10-3 с. Производственные системы и компиляторы пока не появились. В конце этого периода стали выпускаться устройства памяти на магнитных сердечниках. Надежность ЭВМ этого поколения была крайне низкой.
Задача
Представим числа 2110 и -1910 в дополнительном коде.
Представим число 21 в двоичном коде.
21 = 101012
Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Двоичное число 10101 имеет обратный код 0,10101
Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.
Число 21 представляется в двоичном дополнительном коде как 0,10101
Представим число -19 в двоичном коде.
19 = 100112
Двоичное число 10011 имеет обратный код 1,01100
В итоге получаем:
| 5 | 4 | 3 | 2 | 1 | 0 |
Число -19 представляется в двоичном дополнительном коде как 1,01101
Сложим числа 010101 и 101101
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 5 | 4 | 3 | 2 | 1 | 0 |
В 2-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 3-й разряд.
| 5 | 4 | 3 | 2 | 1 | 0 |
В 3-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 4-й разряд.
| 5 | 4 | 3 | 2 | 1 | 0 |
В 4-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 5-й разряд.
| 5 | 4 | 3 | 2 | 1 | 0 |
В 5-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 6-й разряд.
| 5 | 4 | 3 | 2 | 1 | 0 |
В итоге получаем:
| 5 | 4 | 3 | 2 | 1 | 0 |
Результат сложения: 000010
Получили число 000010. В десятичном представлении это число имеет вид:
Для перевода необходимо умножить разряд числа на соответствующую ему степень разряда.
000010 = 25*0 + 24*0 + 23*0 + 22*0 + 21*1 + 20*0 = 0 + 0 + 0 + 0 + 2 + 0 = 2
Результат сложения (в десятичном представлении): 2
БИЛЕТ 17
Date: 2015-09-05; view: 899; Нарушение авторских прав