
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Погрешности численных методов анализа динамики мат моделей систем
Источники погрешностей:
1. может оказаться, что нач усл-я x(t0) известны неточно и опред-ся в рез-те эксперимента или в рез-те реш-я какой-либо другой задачи. В данном случае вместо точного нач. усл-я приходится исп-ть его приближение. А вместо задачи Коши решать задачу 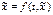 ,
, 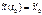 (1.1)
(1.1)
с изменяемыми нач усл-ями 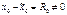 . Т.о., реш-е задачи (1.1) зависит от
. Т.о., реш-е задачи (1.1) зависит от  и не совпадает с искомым реш-ем x(t).
и не совпадает с искомым реш-ем x(t).
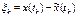 наз-ся неустранимой погрешностью реш-я
наз-ся неустранимой погрешностью реш-я 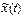 .
.
2. погрешность округления обусловлена ограничениями представления чисел на ЭВМ и как следствие погрешность вычисляется правой части ур-я  (1.2) и по формуле
(1.2) и по формуле 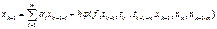 (1.3). Фактически найденные знач-я
(1.3). Фактически найденные знач-я  удовлетворяет не уравнению (1.3), а условию
удовлетворяет не уравнению (1.3), а условию 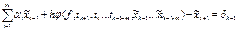
 - наз-ся погрешностью округления на k-том шаге.
- наз-ся погрешностью округления на k-том шаге.
3. погрешность метода или сечения
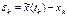 (1.4)
(1.4)
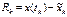 (1.5)
(1.5)
 (1.6)
(1.6)
 (1.7)
(1.7)
Погреш-ть м-да связана с тем, что при аппроксимации ф-ции правой части ур-я (1.2) вместо бесконечных рядов часто исп-ся лишь несколько первых членов. Данная погрешность может быть определена как разность м/у истинным знач-ем реш-я 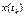 (1.1) и его приближенным знач-ем
(1.1) и его приближенным знач-ем 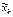 , полученное по ф-ле (1.3).
, полученное по ф-ле (1.3).
(1.4) разность м/у точным реш-ем 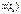 задачи (1.2) и приближенным фактически найденным знач-ем
задачи (1.2) и приближенным фактически найденным знач-ем 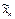 наз-ся полной погреш-тью приближенного реш-я (1.5). (1.6) наз-ся вычислительной погреш-тью. Исходя из соотношений погреш-ти
наз-ся полной погреш-тью приближенного реш-я (1.5). (1.6) наз-ся вычислительной погреш-тью. Исходя из соотношений погреш-ти 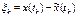 , (1.4), (1.5), (1.6) следует (1.7).
, (1.4), (1.5), (1.6) следует (1.7).
Полная погреш-ть приближенного м-да равна сумме неустранимой погреш-ти, погреш-ти м-да и вычислительной погреш-ти. Указанные источники погреш-ти явл-ся причиной наблюдаемости 2-х ошибок: 1. локальные ошибки; 2. глобальные ошибки.
20. Численные м-ды анализа динамики мат. моделей: одношаговые м-ды реш-я задачи Коши
Пусть требуется найти реш-я задачи  (1.1) на отрезке
(1.1) на отрезке 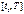 . Разобьем данный отрезок точками
. Разобьем данный отрезок точками  эти точки наз. сеткой, а N узлами сетки.
эти точки наз. сеткой, а N узлами сетки.
Рассмотрим м-ды вида  (1.2), который послед-но дает приближ-е
(1.2), который послед-но дает приближ-е 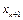 к знач-ю точного реш-я
к знач-ю точного реш-я 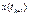 в каждом узле сетки
в каждом узле сетки 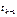 на основе известного приближ-я
на основе известного приближ-я 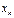 в предыдущем узле
в предыдущем узле  .
.
В общем виде их можно записать: 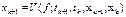
Простейшим одношаговым м-дом явл-ся м-д Эйлера. Он основан на разложении реш-й x(t) в окрестности точки  в ряд Тейлора. Если предположить, что правая часть ур-я f=x(t) диф ур-ем (1.1) имеет непрерывные частные производные до порядка s, то искомые реш-я x(t), также имеют непрерывные производные до (s+1) порядка, при этом точное реш-е в узле
в ряд Тейлора. Если предположить, что правая часть ур-я f=x(t) диф ур-ем (1.1) имеет непрерывные частные производные до порядка s, то искомые реш-я x(t), также имеют непрерывные производные до (s+1) порядка, при этом точное реш-е в узле 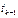 будет иметь вид:
будет иметь вид:
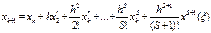 (1.3)
(1.3)

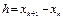
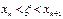
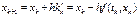 , k=0,1,…,N (1.4)
, k=0,1,…,N (1.4)
Предположение, что h мало можно пренебречь в ур-е (1.3) членами содержащими h во II или более порядками, тогда явный м-д Эйлера может быть определен след образом (1.4). Т.о., можно получить приближенное знач-е зависимой перем-ой при малом смещении h от текущей точки. Следует отметить, что разлож-е x(t) в ряд Тейлора, аналогично (1.4) можно выполнить и в окрестности точки 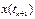 .
.
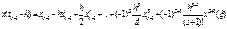 (1.5)
(1.5)
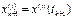 ,
, 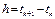
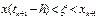
М-ды, полученные по этой ф-ле, образуют семейство одношаговых м-дов. Простейшим из них явл-ся неявный м-д Эйлера, получаемый из ур-я (1.5).
Нем. математик Рунге предложил след. идею, основанную на вычислении приближенного реш-я  в узле
в узле  в виде лин-ой комбинации с постоянными коэф-тами:
в виде лин-ой комбинации с постоянными коэф-тами:
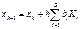 (1.6)
(1.6)
где  ,
, 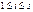
Числа 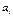 ,
,  ,
,  выбираются так, чтобы разлож-е выраж-я (1.6) по степеням h совпало с разлож-ем (1.3) или (1.5) до максимально возможной степени при произвольной правой части и произвольном шаге h. Если ввести вспомогательную функцию
выбираются так, чтобы разлож-е выраж-я (1.6) по степеням h совпало с разлож-ем (1.3) или (1.5) до максимально возможной степени при произвольной правой части и произвольном шаге h. Если ввести вспомогательную функцию  , то разлож-е по степеням h должно начинаться с max возможной степени.
, то разлож-е по степеням h должно начинаться с max возможной степени.
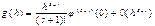
Величина φ(h) наз погрешностью м-да на данном шаге или локальной погреш-тью м-да.
Ф-ла (1.6) образует семейство м-дов Рунге-Кутта порядка s и для их реализации требуется s вычислений функции f(t, x(t)), представляющих собой производные реш-я.
Если  =0 при j≥i для всех i, то
=0 при j≥i для всех i, то 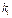 вычисляется в явном виде. Если
вычисляется в явном виде. Если 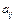 =0 при j>i и
=0 при j>i и  , то каждая
, то каждая 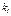 неявно определяется ур-ем:
неявно определяется ур-ем:  . В данном случае необходимо каким-либо способом вычислить
. В данном случае необходимо каким-либо способом вычислить  , например, с помощью итерации по м-ду Ньютона.
, например, с помощью итерации по м-ду Ньютона.
Примером явного м-да Рунге-Кутта явл-ся м-д Хойна, к-рый в случае, если правая часть ур-я (1.1) не зависит от t переходит в квадратичную форму трапеции, при этом s=2, a11=0, a12=0, a21=1, a22=0, b1=b2=0,5, c1=0, c2=0.
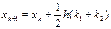 ,
, 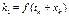 ,
, 
Всем одношаговым м-дам присуще общие черты: 1. чтобы получить инф-цию о новом узле необх-мо иметь инф-цию об одном предыдущем; 2. в основе всех одношаговых м-дов лежит разлож-е функции правой части ур-я (1.1) в ряд Тейлора; 3. все одношаговые м-ды не требуют действительного вычисления производной, вычисляется лишь сама функция, знач-е к-рой могут потребоваться в неск-ких промежуточных точках.
22. Анализ статики математических моделей систем
Задача анализа статики возникает обычно при определении статических характеристик системы или начальных условий для задачи анализа динамики и, как правило, предшествует последней. Поэтому основной целью расчета статики является определение неизвестных векторов выхода У=у(t) и состояния x=x(t) по заданным постоянным значениям вектора входа u=u(t) для фиксированного момента времени при условии, что x(t)=0. В зависимости от вида вектор-функции, описывающей связи в ММС. для заданных и. и /* может быть несколько статических режимов. В этом случае ММС называется многостабильной и решение задачи анализа статики неоднозначно.
Существует несколько подходов к решению задач анализа статики.
Первый подход (метод установления) основан на численном интегрировании исходной системы обыкновенных дифференциальных уравнений. Решение такой системы при неизменном векторе входов с некоторых исходных значений состояния через достаточный промежуток моделируемого времени должно привести
к приближенно стационарной точке, в которой х(t.)=0. Эта точка и будет точкой решения y(t,), x(t.).
Подход к анализу статики через интегрирование дифференциальных уравнений численными методами получил достаточно широкое распространение, так как позволяет с помощью одних и тех же методов решать как статические, так и динамические задачи. Однако при этом, как правило, получаются завышенные затраты машинного времени.
Более экономичны подходы, в которых в качестве ММС берется система нелинейных алгебраических уравнений (СНАУ):
F(v)=0, (1.1)
где v — вектор неизвестных, F — заданная вектор-функция.
Второй подход (итерационный) основан на применении методов решения СНАУ. В большинстве случаев эти методы являются итерационными. При этом задаются начальным приближением v0 и выполняют ряд однотипных итераций. Если вектор приближений на k-oй итерации vk стремится к вектору решения vk то говорят, что метод сходится.
В третьем подходе к решению задач анализа статики последние представляются как экстремальные. Для этого образуется скалярная целевая функция, имеющая минимум в точке решения задачи vk.
Вычисление и. производится с применением методов оптимизации
23. Аналитические методы анализа статики мат моделей: метод возмущений.
Аналитические методы
Аналитические методы для СНАУ (1.1) позволяют получить решение в виде формул. Точные методы позволяют получить решение, используя аналитические (формульные) зависимости. Приближенные методы основаны на построении аналитических зависимостей, аппроксимирующих решение.
Метод возмущений
Пусть требуется найти решение СНАУ вида
F(x, е)=0,
где x — неизвестный вектор, е — числовой малый параметр. Предположим, что при е=0 система может быть сравнительно легко решена и найдено приближение х0. Возьмем в качестве нового приближения к решению x, x= x0+ex1. Подставим х в (1.6) и разрешим ее относительно Х1. Продолжая аналогично, можно получить некоторый итеративный процесс, при котором решение (1.6) представляется в виде
х= 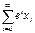
Если при e=0 вектор-функция F{x, 0) хорошо приближает F(x,е), то методы подобного типа оказываются весьма эффективными на практике.
24 Метод асимптотических разложений
В случаях, когда нельзя получить начальное приближение решения Хо, положив е=0, или при вырожденности матрицы
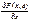 можно получить решение в виде ряда
можно получить решение в виде ряда
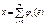
где φ—некоторые функции, зависящие от малого параметра, которые строятся таким образом, чтобы выполнялось условие

Ряд при этом называется асимптотическим разложением решения х.
25 Численные методы
При решении задач анализа статики ММС (1.1) основным инструментом являются численные методы, позволяющие свести решение к выполнению конечного числа арифметических действий над числами. При этом результаты получаются также в виде чисел.
При численном решении СНАУ (1.1) следует учитывать, что не существует математических результатов, позволяющих в общем виде решить вопрос о существовании и числе решений. Поиск решения можно представить как поиск в пространстве Rk точек, общих для k поверхностей, каждая из которых задается уравнением системы.
Другой важной особенностью численного решения системы является то, что из-за нелинейности ММС в общем случае нельзя применять прямые методы (например, метод последовательного исключения). Поэтому разработанные методы решения являются итерационными: начиная с начального вектора последовательно приближаются к решению с помощью итерационной процедуры
вида
Этот метод состоит в следующем: система уравнений преобразуется к виду
v=G(v)
и итерации проводятся по формуле
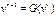 г=0, 1....
г=0, 1....
1.2.2. Метод Ньютона и его модификации
Если известно достаточно хорошее начальное приближение v° к решению системы, то эффективным для повышения точности является метод Ньютона, основанный на замене в окрестности vr исходной нелинейной задачи некоторой вспомогательной линейной задачей.
1.2.3. Метод продолжения по параметру
Этот метод представляет собой алгоритм, позволяющий с помощью итераций получить решение СНАУ (1.1). Его эффективность не зависит от «удачного» выбора начального приближения. Суть метода состоит в том, что наряду с исходной системой (1.1) рассматривается другая:
G(v)=0,
решение которой известно. Затем, «деформируя» уравнение, превратим его в с помощью конечного числа Л' последовательных малых приращений параметров:
Gr(v) = С  (v) + [F(v) — Gr-l(v)]
(v) + [F(v) — Gr-l(v)]
21. Многошаговые методы решения задачи Коши
Рассматриваются численные методы решения з-чи Коши. При этом значение решения xk в точке tk опред через значение решения в m точках, предшествующих tk. Такой метод наз m-шаговым. Из этого класса выделяются линейные многошаговые методы вида
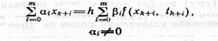 применяемые на сетке с пост шагом tk=o+hk, k= =0, 1,..., N. Разность между наибольшим и наименьшим значениями индекса неизвестной ф-ции Xk из равна m. Поэтому ур-ие явл разностным ур-нием m-го порядка, общее решение к-ого зависит от m параметров. Чтобы выделить ед-нное решение этого у-ния, необходимо задать m дополнит-ых условий на ф-ию Xk к-ыми явл знач-я ф-ии Xk при к=0, 1,..., m —1 и предполагаются известными. Т.о. численные методы данного класса состоят в р-ии разностной з-чи Коши для разностного ур-ия; Если искомое р-ние Xk+m входит в правую часть ур-ния (bm≠0), то метод наз. неявным. В Противном случае (bm≠0) ур-ние может быть явно разрешено относительно Хкт. В этом случае определяет явный метод. Методы, задаваемые часто называются конечно-разностными схемами.
применяемые на сетке с пост шагом tk=o+hk, k= =0, 1,..., N. Разность между наибольшим и наименьшим значениями индекса неизвестной ф-ции Xk из равна m. Поэтому ур-ие явл разностным ур-нием m-го порядка, общее решение к-ого зависит от m параметров. Чтобы выделить ед-нное решение этого у-ния, необходимо задать m дополнит-ых условий на ф-ию Xk к-ыми явл знач-я ф-ии Xk при к=0, 1,..., m —1 и предполагаются известными. Т.о. численные методы данного класса состоят в р-ии разностной з-чи Коши для разностного ур-ия; Если искомое р-ние Xk+m входит в правую часть ур-ния (bm≠0), то метод наз. неявным. В Противном случае (bm≠0) ур-ние может быть явно разрешено относительно Хкт. В этом случае определяет явный метод. Методы, задаваемые часто называются конечно-разностными схемами.
В качестве примеров рассмотрим часто используемые методы прогноза и коррекции. В методе Милна на этапе прогноза испол формула

а на этапе коррекции — формула Симпсона:
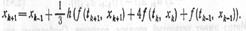
Этот м-д относится к м-дам четвертого порядка точности. практич-их расчетах м-д Милна использ реже, чем др., т.к ему присуща неустойчивость Это означает, что сумарная погрешность может расти экспоненциально, особенно при интегрировании на больших интервалах [t0, Т].
М-д Адамса — Башфорта также имеет четвертый порядок точности. Использ в нем ф-ла прогноза получена интегрированием обратной интерполяционной ф-лы Ньютона и имеет вид
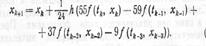
этапе коррекции испол-ся ф-ла
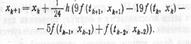
Расчеты по этому м-ду аналогичны м-ду Милна, однако ф-ла явл-ся устойчивой.
В м-де Хэмминга испол-ся ф-лы прогноза:
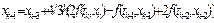
и коррекции:

М-д имеет 4 порядок точности. Особенность его в том что он позволяет оценивать погрешности, вносимые на стадиях прогноза и коррекции, и устранять их. Благодаря простоте и устойчивости этот метод является наиболее распространенным среди применяемых в практических расчетах.
Отдельный класс методов вида составляют методы, основанные на формулах дифф-ния назад (ФДН) [Общий вид этих формул:
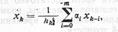
где hk==tk — tk-i — величина к-го шага интегрирования, ai — коэффициенты, величина которых зависит от порядка m формулы (2.44) и значений т предшествующих шагов интегрирования
26. теорема о сжимающем отображении: пусть Н – оператор, отображающий областьД. Если для некоторой нормы существует 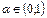 такое что
такое что  (1)при х и у принадлежащим Д, то существует единственная и неподвижная точка
(1)при х и у принадлежащим Д, то существует единственная и неподвижная точка 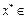 Д, что Н(
Д, что Н(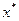 )=
)= 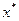 . Для любых
. Для любых 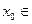 Д последовательность
Д последовательность  удовлетворяет соотношению
удовлетворяет соотношению 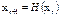 ,r=0,1,2… сходится линейно к
,r=0,1,2… сходится линейно к 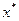 с соnst
с соnst 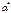 . Для любого
. Для любого 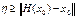 ,
, 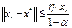
Итерационная ф-ция Н удовлетворяет условию (1) называется сжимающей в обл. Д, т.е. из данного св-ва следует, что начиная из любой данной точки 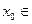 Д длина шага
Д длина шага 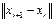 уменьшается при каждой итерации по крайней мере на сомножитель
уменьшается при каждой итерации по крайней мере на сомножитель 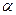 т.к.
т.к. 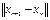 =
= 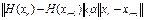 . Теорема может быть использована только для установления линейной сходимости.
. Теорема может быть использована только для установления линейной сходимости.
27. численные методы анализа статики математических моделей систем: метод продолжения по параметру. Суть м-да состоит в том, что наряду с исходной с-мой F(x; 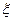 )=0(1) рассматривается и другая G(v)=0,решение кот. известно. Затем деформируя это уравнение, его превращают в (1) с помощью конечного числа N последовательно малых приращений:
)=0(1) рассматривается и другая G(v)=0,решение кот. известно. Затем деформируя это уравнение, его превращают в (1) с помощью конечного числа N последовательно малых приращений: 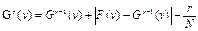 . Решение V
. Решение V 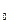 можно использовать как исходное значение переменных для итерационного решения ур-я V(v)=0. В процессе счета реш-е
можно использовать как исходное значение переменных для итерационного решения ур-я V(v)=0. В процессе счета реш-е 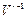 используется как исходное решение
используется как исходное решение 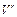 . Когда r=N то решаемая сис-а Ур-ний становится эквивалентной исходной. Если исх-е Ур-е(1) не содержит параметров позволяющих получить сис-у G(v)=0 то его можно ввести искусственно следующим образом:
. Когда r=N то решаемая сис-а Ур-ний становится эквивалентной исходной. Если исх-е Ур-е(1) не содержит параметров позволяющих получить сис-у G(v)=0 то его можно ввести искусственно следующим образом: 
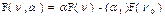 , где
, где 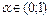 - вводимый параметр.
- вводимый параметр.  - начальное приближение при
- начальное приближение при  система преобразуется к виду аналогичному G(v)=0, а при
система преобразуется к виду аналогичному G(v)=0, а при  - к исходной системе.
- к исходной системе.
28. понятие имитационного моделирования. Имитац-е мод-е представляет собой численный м-д вычисл-х экспериментов с ММ имитирующими поведения реальных объектов, процессов и систем во времени течении заданного периода. При этом функционирование реальных сис-м разбивается на элементарные явления подсистемы и модуля. Их функционирование описывается набором алгоритмов, которые имитируют реальные явления с сохранением их логической структуры и последовательности протекания во времени.
29. Вероятностные аналитические и вероятностные имитационные модели. Одним из видов им.мод. явл-ся статистическое им.мод. Оно позволяет воспроизводить на ЭВМ функционирование сложных случ. процессов. При исследовании сложных систем подверженных случ. воздействиям исп-ся: а) вероятностные аналитич. мод.(ВАМ), б) вероятностные им. мод.(ВИМ). В ВАМ влияние случ. факторов учитывается с помощью задания вероятностных характеристик случ. процессов. В ВИМ оперируют с конкретными случ-ми числовыми значениями параметров. При этом полученные рез. явл-ся случ. реализациями. При реализации на ЭВМ статистич и им.мод. возникает задача получения на ЭВМ случ. числовых значений с заданными вероятностными характеристиками.
30. Программные средства для решения задач моделирования. При решении задач в мод-и анализа и синтеза САУ исп-ют различ. прог. ср-ва предназначенные для матеметич. выч-ий в тех. приложениях- MATLAB, MATCAD, EXCEL и т.д. Система MATLAB создана как язык программирования высокого уровня для тех. вычислений. Система имеет открытую архитектуру и современные версии, поставляется вместе с пакетом расширения Sumlink. В системе реализован принцип визуально-ориентированного программирования. Уравнения состояний описывающие динамич. системы формируются автоматически. Имеются виртуальные средства регистрации и визуализации результатов моделирования. Ф-ция системы позволяет в интерактивном движении выполнять сложные математич. вычисл-я, разрабатывать алгоритмы, выполнять эксперименты и им.мод. AnyLogic графическая среда для моделирования слож. дискретных непрерывных систем, а так же нескольких движущихся объектов, которые исчезают и появляются при взаимодействии друг с другом. Dynast программное обеспечение для расчета переходных процессов символического и частного анализа линеаризованных систем, описываемые системой диф. ур-ий, алгебраических ур-ий и блок схемами. М.В.Т.У.-программа моделирования в тех. устройствах является отечественной разработкой с классич. интерфейсом блочного моделирования. SamSim моделирование линейных и нелинейных цепей, построение временных, частотных характеристик, фазовых портретов и годографов. Копрас-комплекс программ для решения задач анализа и синтеза автоматич. систем.
Date: 2015-09-05; view: 349; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |