
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дискретно-стохастические модели (Р-схемы)
|
|
В общем виде вероятностный автомат можно определить как дискретный контактный преобразователь, функционирование которого в каждом такте зависит только от состояния памяти, в нем и может быть описан статически. Применение вероятностных автоматов имеет важное значение для разработки методов проектирования дискрет систем. Также для выяснения агоритмических возможностей систем для обоснования границ целесообразности использования таких систем, а также для решения задач синтеза по выбранным критериям дискретных стохастич-х систем. Рассмотрим множ-во G элементами которого являются все возможные пары (xi, zc) где x и z соответствующие элементы внутр состояния и элементы подмножества входных сигналов. Если сущест-т две ф-ции φ,ψ, то с их помощью осуществляется отображение G→y; G→z и говорят, что F=< z,x,y,Z,φ,ψ> определяется автомат детерминированного типа. Пусть Ф-множество всевозможных пар вида: (zk, yi), где yi -- входное подмножество. Пусть в любой момент вр, любой эл-т множ-ва G, реализовывая на множестве Ф некоторые законы распределения:
элементы Ф (z1,y1) (z1,y2) (zk,yj-1) (zk,yj)
(xi, zs) b11 b12 bk(j-1) bkj
При этом сумма всех b=1. Где bj – вероятность перехода автомата в состояние Gk и появления на выходе сигнала. Если он был в состоянии Gs и на его вход подавался сигнал xi. Число таких распределений представляется в виде таблицы равное числу элементов множества G. Обозначим множество этих таблиц через В, тогда четверка элементов Р<х,у,z,В> называется вероятностным автоматом. Пусть элементы подмнож-ва G реализуют некоторый закон распределения на подмножества у и z. Это можно представить:
эл-ты из у у1 у2 уj-1 yj
(xi, zs) q1 q2 qj-1 qj
эл-ты из z z1 z2 zk-1 zk
(xi, zk) z1 z2 zk-1 zk
zk, qk - вероятности перехода P-автомата состояния zk и появления выходного сигнала yk при условии, что Равтомат находится в состоянии zs и на его вход подается сигнал xi
Если для всех k и Gимеет место соотношение qk zi=bk, то это автомат Мили. Это требование означает выполнение условия независимости распределения нового состояния Равтомата и его вых сигналов. Пусть теперь определение вых сигн Р автомата зависит лишь от того состояния, в котором находится автомат в данн момент вр. Пусть кажд эл-т выходного подмнож-ва реализуют распределение вероятностивыхода и имеет след вид:
эл-ты из у у1 у2 ук
Zk s1 s2 sk
Здесь, где si – вероятность появления вых сигнала уi, при условии, что автомат находится в состоянии zk.
16. Аналитические методы анализа динамики мат. моделей систем: м-д возмущений.
Рассмотрим динамику популяций 2-х видов, взаимодействующих м/у собой по типу «хищник-жертва». Построим мат.модель, предполагая, что жертва может найти достаточно пищи для пропитания, но при каждой встрече с хищником последний убивает жертву.
х(t)-кол-во жертв; y(t)-кол-во хищников, xB-кол-во рожденных жертв, xd-естественная смертность жертв,
(xB-xd)*x(t) – скорость пополнения популяции жертв
x(t)*y(t) – число случаев, когда хищник убивает жертву, зависит от вероятности их встречи.
 уравнение Лотки-Вольтерра
уравнение Лотки-Вольтерра
где γ<0, δ>0, γ - естественная смертность, δ - вероятность встреч.
Для полной постановки задачи зададим рассматриваемый промежуток времени 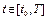 , тогда кол-во хищников и кол-во жертв в нач время x(t0)=x0, y(t0)=y0
, тогда кол-во хищников и кол-во жертв в нач время x(t0)=x0, y(t0)=y0
Поскольку аналитическое представление реш-я задачи (1.1) и (1.2) затруднительно, то используют приближенный м-д, основанный на теории возмущ-я.
Первый шаг состоит в определении стационарных точек (xS, yS), к-рые также наз-ся точками равновесия. В данном случае стац сост-е будет определяться:
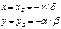
т.к 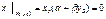
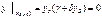 , то
, то
разложив равные части в ряд Тейлора, получим:
x(α+βy)=βxS(y-yS)…
y(γ+δx)=δyS(x-xS)…
В окрестности данной точки мы можем разбить исх. ур-я лин-ми:
x=βxS(y-yS)
y=δyS(x-xS), используя аппарат высшей математики, получим:
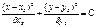
На рис. показано семейство подобных эллипсов с центром в точке (xS, yS), причем стрелками указываются направ-я соответствующие возрастанию времени.
17. Аналитический метод анализа динамики мат. моделей сис-м: м-д асимптотических разложений.
Рассмотрим задачу нахожд-я реш-й ММ сис-ы, описываемые диф. ур-ем:
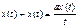
для больших t (t>>1)
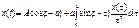 (1.1)
(1.1)
Известно, что интеграл сходится при t→ ∞ следовательно принимаем t=∞
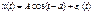 (1.2)
(1.2)
Если ур-е (1.2) подставим в ур-е (1.1), то получим:
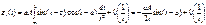
Получим второе приближение:
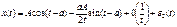 (1.3)
(1.3)
это выраж-е (1.3) подставим в (1.1), получим:
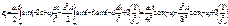
1 интеграл преобразовывается интегрированием по частям, а второе – по формуле тригонометрии, оставшиеся интегралы входят в величину 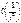
3 приближение:
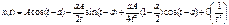
Date: 2015-09-05; view: 383; Нарушение авторских прав