Параметр потока отказов

Простейшая модель описания потоков отказов и восстановлений, при которой элемент или привод функционирует до первого отказа случайное время 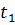. Затем следует его мгновенное восстановление в момент времени 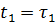, после чего элемент работает случайно в течение времени 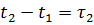до второго отказа и т.д. Моменты времени образуют случайный поток отказов.

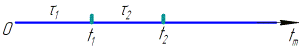
Рисунок 8 – Модель описания потоков отказов

Процесс восстановления описывается случайной величиной 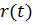, равной числу отказов, произошедших за время 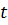. Величину 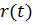на интервале можно характеризовать математическим ожиданием числа отказов 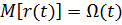, которое называется ведущей функцией потока или функцией восстановления.

Также используют производную математического ожидания числа отказов – параметр потока отказов:

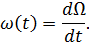
Статистически параметр потока отказов определяется:

где 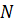- число наблюдаемых элементов;

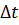- промежуток времени;

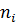- число отказов.

Параметр потока отказов (по времени) сначала возрастает, потом начинает колебаться с затуханием на уровн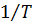е , где 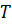- средняя наработка между отказами.

При статистической оценке

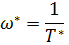
это среднее число отказов восстанавливаемого элемента в единицу времени, т.е. это показатель надежности восстанавливаемых изделий, равный отношению среднего числа отказов изделия за произвольную малую его наработку к значению этой наработки (соответствует интенсивности отказов для неремонтируемых изделий, но включает повторные отказы).

Частота отказов представляет собой плотность распределения вероятностей наработки между отказами и определяется статистически. Является отношением количества отказов однотипных восстанавливаемых систем (элементов) 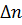в течение интервала времени 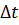к произведению первоначального количества рассматриваемых систем 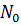и времени :

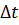Интенсивность отказов в случае восстанавливаемых систем определяется как:

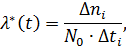
где 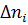- число отказавших элементов;

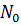- число элементов данного типа в системе, остающееся всегда постоянным.

Средняя наработка на отказ в вероятностной форме определяется как:

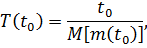
где 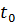– суммарная наработка за заданное время ;

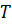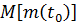- математическое ожидание числа отказов за это время.

Средняя наработка на отказ в статистической форме определяется как:

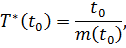
где 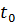- суммарная наработка элемент за время наблюдения;

- число отказов за это время.

Средняя наработка между отказами в вероятностной форме:

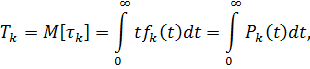
где - плотность распределения вероятности наработки между отказами;

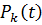- функция надежности наработки между отказами.

Средняя наработка между отказами при статистической оценке:

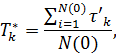
где 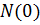- общее число элементов, начавших работать после (k-1)-го восстановления;

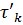- время работы после (k-1)-го восстановления до k-го отказа i-го элемента.

Среднее время безотказной работы определяется как математическое ожидание времени наработки между отказами:

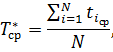
где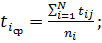

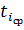- среднее время наработки между отказами каждого из N-го числа испытуемых систем;

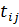- наработка между последующим и предыдущим отказами системы;

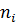- число отказов системы в течение заданного времени.

Интенсивность восстановления при статистической оценке есть отношение числа восстановлений в период времени 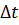к произведению числа элементов 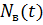, не восстановленных к моменту времени 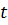, на длительность интервала времени :

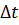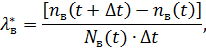
где 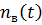- число элементов, восстановление которых длилось меньше времени ;

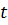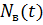- число элементов, восстановление которых длилось больше времени .

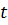Среднее время восстановления при вероятностной оценке выражается как:

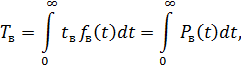
где 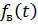- плотность распределения времени восстановления ;

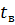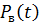- вероятность восстановления за заданное время.

При статистической оценке:

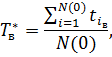
где 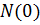- общее число элементов, подвергшихся восстановлению;

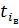- среднее время восстановления i-го элемента.

Вероятность восстановления представляет собой значение функции распределения вероятности восстановления за заданное время 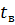, определяется формулой Пуассона:

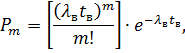
где 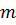- число восстановлений;

- интенсивность восстановления.

Коэффициент готовности – это комплексный показатель, т.к. количественно характеризует одновременно два показателя – безотказность и ремонтопригодность:

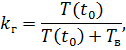
где 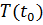- средняя наработка на отказ;

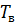– среднее время восстановления одного отказа.

Коэффициент технического использования характеризует долю времени нахождения элемента в работоспособном состоянии относительно рассматриваемой продолжительности эксплуатации, учитывает затраты времени на плановые и внеплановые ремонты:

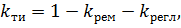
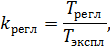
где 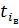- время восстановления i-го элемента;

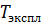- время эксплуатации элемента;

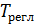- время, затраченное на проведение всех видов регламентных работ, предусмотренных документацией.

Вероятность безотказной работы восстанавливаемого привода есть вероятность того, что привод в любой момент времени находится в работоспособном состоянии.

Выражение вероятности безотказной работы имеет вид:

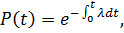
куда при расчете восстанавливаемого привода вместо 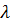подставляют 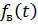или .

Восстанавливаемый привод в произвольный интервал времени 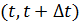будет в работоспособном состоянии в конце интервала 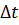только при выполнении несовместных событий:

А – привод работоспособен в момент времени 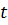и на интервале 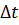не откажет;

В – привод к моменту времени 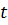отказал, но на интервале 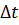восстановлен.

Тогда вероятность этих двух событий будет иметь вид:

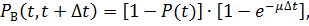
где 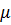- параметр восстановлений (аналогичен параметру потока отказов) – величина, обратная времени восстановления :

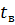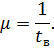
При учете, что события А и В несовместные, из решения уравнения 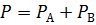получим:

Применив предельный подход 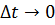и начальное условие , получим выражение для определения вероятности работоспособного состояния восстанавливаемого привода в любой момент времени:

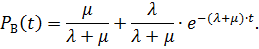
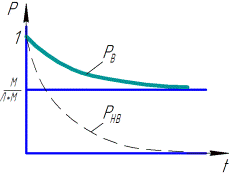
Рисунок 9 – Зависимость вероятности безотказной работы для восстанавливаемых и невосстанавливаемых приводов

Из Рисунка 9 видно:

· минимальная вероятность безотказной работы восстанавливаемого привода ограничивается параметром восстановления 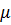, т.к. ;

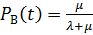· вероятность безотказной работы восстанавливаемого привода выше, чем невосстанавливаемого;

· чем меньше 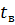(больше 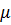), тем больше вероятность безотказной работы.

Вероятность отказа определяется по формуле:

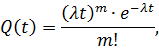
где 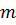- число отказов;

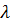- параметр потока отказов;

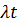- математическое ожидание числа отказов.

Для восстанавливаемых объектов периоды потери работоспособности назначаются заранее определенной системой планово-предупредительных ремонтов и технического обслуживания, проводимых в определенные моменты времени. В этом случае поток отказов не носит случайных характер, а является заранее запланированным. Потоки отказов и восстановлений являются критериями для назначения планово-предупредительных ремонтов и длительности периода между техническим обслуживанием.

Date: 2015-09-05; view: 2011; Нарушение авторских прав