
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

п.1.Формула Муавра
|
|
Теорема. (Формула Муавра, 1707 г.)
Для любого целого числа n и любого действительного числа 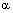 имеет место следующее равенство:
имеет место следующее равенство:
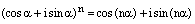 . (1)
. (1)
Доказательство. Разобьем доказательство на 3 этапа.
1) Пусть 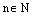 – натуральное число. Так как комплексное число
– натуральное число. Так как комплексное число 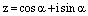 имеет модуль
имеет модуль 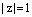 , то справедливость формулы Муавра в этом случае следует из следствия 2 теоремы об умножении комплексных чисел в тригонометрической форме записи.
, то справедливость формулы Муавра в этом случае следует из следствия 2 теоремы об умножении комплексных чисел в тригонометрической форме записи.
2) Пусть теперь 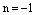 . Тогда
. Тогда
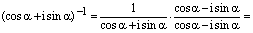
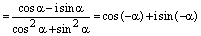 , ч.т.д.
, ч.т.д.
3) Пусть 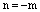 , где
, где 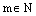 – натуральное число. Тогда по свойству целых степеней, которые справедливы в любом поле, в том числе и в полекомплексных чисел, имеем:
– натуральное число. Тогда по свойству целых степеней, которые справедливы в любом поле, в том числе и в полекомплексных чисел, имеем:
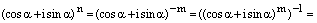
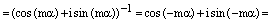
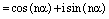 .
.
Теорема. (О делении комплексных чисел в тригонометрической форме)
Пусть 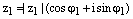 , где
, где 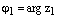 и
и 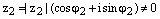 , где
, где 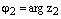 – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
– два произвольных комплексных числа записанных в тригонометрической форме. Тогда
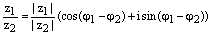 . (2)
. (2)
Доказательство. Воспользуемся следствием формулы Муавра и правилом умножения комплексных чисел в тригонометрической форме записи. Получаем:
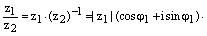
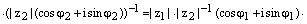
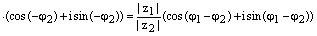 , ч.т.д.
, ч.т.д.
Пример 1. Запишите комплексные числа 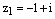 и
и 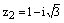 в тригонометрической форме и найдите их произведение
в тригонометрической форме и найдите их произведение 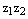 и частное
и частное 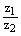 .
.
Решение. 1) Комплексное число 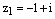 на комплексной плоскостинаходится во второй четверти, поэтому
на комплексной плоскостинаходится во второй четверти, поэтому
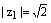 ,
, 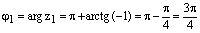
17) Многочлен с одной переменной – это многочлен вида:
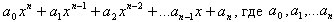 , где - коэффициенты, а х – переменная.
, где - коэффициенты, а х – переменная.
Примеры:
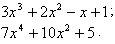 .
.
Самая большая степень у переменной, у которой коэффициент не равен 0 - степень многочлена.
Пример:
0x^2+x+1 - степень равна 1
y-y^3+1 - степень равна 3.
19)
Теорема Безу утверждает, что остаток от деления многочлена P(x) на двучлен x − a равен P(a).
Предполагается, что коэффициенты многочлена содержатся в некотором коммутативном кольце с единицей (например, в поле вещественных или комплексных чисел).
Схе́ма Го́рнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корни многочлена[1], а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида x− c. Метод назван в честь Уильяма Джорджа Горнера (англ.).
Задан многочлен P(x):
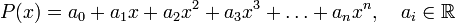 .
.
Пусть требуется вычислить значение данного многочлена при фиксированном значении x = x0. Представим многочлен P(x) в следующем виде:
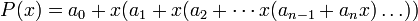 .
.
Определим следующую последовательность:
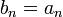
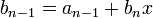
…
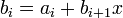
…
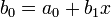
Искомое значение P(x0) = b0. Покажем, что это так.
В полученную форму записи P(x) подставим x = x0 и будем вычислять значение выражения, начиная со внутренних скобок. Для этого будем заменять подвыражения через bi:
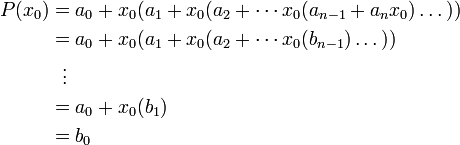
Если рациональное число (несократимая дробь)
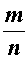 ,
,
где 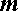 – число целое, а
– число целое, а 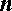 – число натуральное, является корнем многочлена
– число натуральное, является корнем многочлена 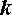 -ой степени
-ой степени

все коэффициенты
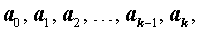
которого являются целыми числами, то числитель дроби 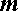 является делителем коэффициента
является делителем коэффициента 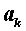 , а знаменатель дроби
, а знаменатель дроби 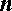 является делителем коэффициента
является делителем коэффициента 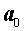 .
.
Коэффициент 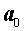 называют старшим коэффициентом многочлена, а коэффициент
называют старшим коэффициентом многочлена, а коэффициент 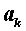 - свободным членом многочлена.
- свободным членом многочлена.
Вектор – направленный отрезок. Другими словами, вектором называется отрезок, для которого указано, какой из его концов является началом, а какой концом.
На рисунках направление вектора обозначается стрелкой от начала к концу. Если длина рассматриваемого отрезка равна нулю, то есть отрезок вырождается в точку, то эта точка тоже может рассматриваться как вектор. Такой вектор называется нулевым и имеет произвольное направление.
Определение 9.2.
Длиной (модулем) ненулевого вектора  называется длина отрезка AB. Она обозначается как
называется длина отрезка AB. Она обозначается как 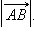 Длина нулевого вектора равна нулю:
Длина нулевого вектора равна нулю: 
Определение 9.3.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Поскольку нулевой вектор может иметь произвольное направление, то разумно считать его коллинеарным любому ненулевому вектору.
Определение 9.4.
Если два ненулевых вектора  и
и 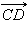 коллинеарны, а лучи AB и CD сонаправлены, то векторы
коллинеарны, а лучи AB и CD сонаправлены, то векторы  и
и 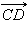 называются сонаправленными. Этот факт обозначается так:
называются сонаправленными. Этот факт обозначается так: 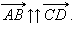 Если же эти лучи не являются сонаправленными, то векторы
Если же эти лучи не являются сонаправленными, то векторы  и
и 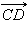 называются противонаправленными. Этот факт обозначается так:
называются противонаправленными. Этот факт обозначается так: 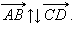
Суммой двух векторов 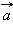 и
и 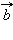 называется новый вектор
называется новый вектор 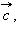 который обозначается
который обозначается 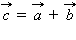 и получается следующим образом.
и получается следующим образом.
Разностью векторов 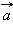 и
и 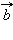 называется такой вектор
называется такой вектор 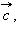 сумма которого с вектором
сумма которого с вектором 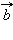 равна вектору
равна вектору 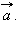 Обозначается разность векторов так:
Обозначается разность векторов так: 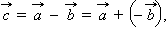 где
где  – вектор, противоположный вектору
– вектор, противоположный вектору 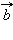 (рис. 9.1.6).
(рис. 9.1.6).
Для коллинеарности вектора 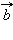 ненулевому вектору
ненулевому вектору 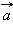 необходимо и достаточно, чтобы существовало такое число λ, что
необходимо и достаточно, чтобы существовало такое число λ, что 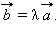
Эта теорема доказывается аналогично, как в планиметрии.
Угол между векторами
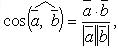
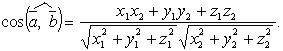
24) рямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.
Положение любой точки в пространстве можно определить при наличии трех взаимнопер-пендикулярных плоскостей, называемых координатными плоскостями; линии их пересечения называются осями координат, точка О их пересечения - началом координат.
Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
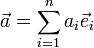
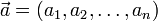
где 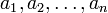 — координаты вектора.
— координаты вектора.
Проведем через точки 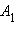 и
и  прямые, параллельные оси z. Пусть эти прямые пересекут плоскость xy в точках
прямые, параллельные оси z. Пусть эти прямые пересекут плоскость xy в точках 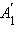 и
и  Заметим, что поскольку эти точки лежат в плоскости xy, то координата z у них равна нулю. Проведем плоскость через точку
Заметим, что поскольку эти точки лежат в плоскости xy, то координата z у них равна нулю. Проведем плоскость через точку 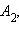 параллельную плоскости xy. Пусть эта плоскость пересекает прямую
параллельную плоскости xy. Пусть эта плоскость пересекает прямую 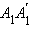 в точке C. Применим теорему Пифагора к треугольнику
в точке C. Применим теорему Пифагора к треугольнику 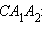
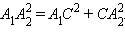 Очевидно, что отрезки
Очевидно, что отрезки 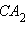 и
и 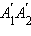 равны, а согласно теореме Пифагора на плоскости xy, получаем, что
равны, а согласно теореме Пифагора на плоскости xy, получаем, что 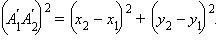 Поскольку длина отрезка
Поскольку длина отрезка 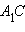 равна
равна 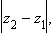 то окончательно имеем
то окончательно имеем 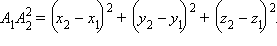
Если же окажется, что отрезок 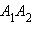 параллелен оси z, то
параллелен оси z, то 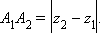 Но тот же результат дает полученная формула, так как в этом случае
Но тот же результат дает полученная формула, так как в этом случае 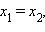
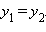
Если x1 и y1 - координаты точки A, а x2 и y2 - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении 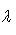
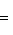
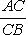 , определяются по формулам
, определяются по формулам
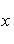
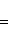
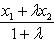
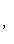
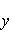
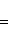
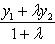

Если 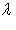
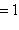 , то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам
, то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам
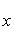
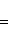
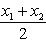

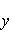
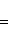
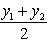
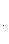
2. Площадь треугольника по известным координатам его вершин A(x1, y1), B(x2, y2), C(x3, y3) вычисляется по формуле

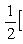
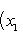
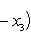
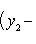
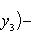
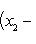
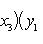
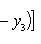
Полученное с помощью этой формулы число следует взять по абсолютной величине.
3. Площадь многоугольника с вершинами A(x1, y1), B(x2, y2), C(x3, y3),..., F(xn, yn) равна
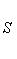
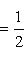
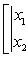

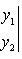
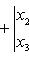
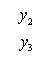
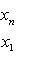
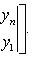
Выражение вида 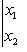
 равно x1y2 - x2y1 и называется определителем второго порядка.
равно x1y2 - x2y1 и называется определителем второго порядка.
Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.
Скалярное произведение векторов - это операция над двумя векторами, результатом которой является число (не вектор).
Определяется скалярное произведение, как правило, следующим образом:
Иными словами, скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними. Необходимо заметить, что угол между двумя векторами - это угол, который они образуют, если отложить их от одной точки, то есть начала векторов должны совпадать.