Первообразная и непосредственный интеграл от функции

Первообра́зной ^[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция 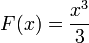является первообразной 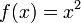. Так как производная константы равна нулю, будет иметь бесконечное количество первообразных; таких как 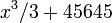или … и т. д.; таким образом семейство первообразных функции x ² можно обозначить как F (x) = x ³ / 3 + C, где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.

Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

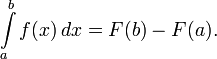
Это соотношение называется формулой Ньютона — Лейбница.

Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:

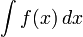
Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G (x) = F (x) + C для всех x. Число C называют постоянной интегрирования.

Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:

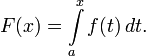
Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, 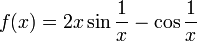с f (0) = 0 не непрерывна при x = 0, но имеет первообразную с F (0) = 0.

Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:

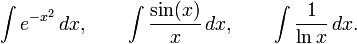
Date: 2015-09-05; view: 449; Нарушение авторских прав