Числовые характеристики непрерывных случайных величин

Определение. Математическим ожиданием непрерывной случайной величины с плотностью распределения f(x) называется число:

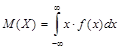, если указанный интеграл абсолютно сходится, в противном случае говорят, что математическое ожидание не существует.

Если н.с.в. определена на интервале (a;b), то математическое ожидание определяется по формуле:

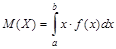
Все свойства математического ожидания дискретных случайных величин справедливы и для непрерывных случайных величин.

Определение. Дисперсией непрерывной случайной величины с плотностью распределения f(x) называется число:

.

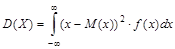Если н.с.в. определена на интервале (a;b), то дисперсия определяется по формуле:

.

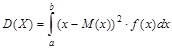Все свойства дисперсии дискретных случайных величин справедливы и для непрерывных случайных величин.

Для непрерывных случайных величин теорема 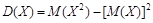может быть записана в виде: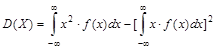

Пример 3. Н.с.в. X задана функцией распределения на интервале . Найти математическое ожидание и дисперсию н.с.в. X.

Найдем плотность распределения: .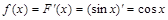

Математическое ожидание: .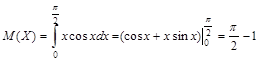

Математическое ожидание квадрата с.в.: .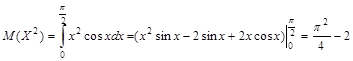

Дисперсия:

Определение. Мода – это значение абсциссы x_mod, при котором кривая плотности распределения имеет максимум. Мода указывает положение высоко вероятной области значений с.в.

Определение. Медиана – это значение абсциссы x_med, при котором фигура под кривой плотности распределения делится на две равновеликие части, площади которых равны по 0.5 каждая, то есть F(x_med)=0.5.

Определение. Квантиль – это значение абсциссы x_q, которое является решением уравнения F(x_q)=q.

Квантиль x_q называется q-ой или q·100-процентной квантилью функции распределения (или плотности распределения, или случайной величины). В частности медиана является 50-процентной квантилью.

Наиболее употребительные квантили:

квартиль - 25 - процентная квантиль, дециль - 10 - процентная квантиль.

Date: 2015-09-05; view: 441; Нарушение авторских прав