Решения в случае нескольких нечетких отношений преимущества

Задача выбора по нескольким отношениям преимущества. Рассмотрим задачу выбора альтернатив по нескольким отношениям преимущества, распространив результаты на нечеткие отношения. Пусть заданно множество альтернатив Х, и качество каждой альтернативы характеризуется несколькими критериями, при этом не оценена непосредственно значением того или иного критерия, а подана в форме соответственных отношений преимуществ на множестве альтернатив.

Таким образом, необходимо осуществить рациональный выбор при условиях наличия информации (Х,R₁,…,R_m) где Х – множество альтернатив, R₁,…,R_m - множество отношений преимущества. В начале рассмотрим простейший случай, а именно когда отношение R_j описывается заданными функциями-критериями Q_j:X®R¹ где R¹ – ось чисел. значение функции Q_j (х) является числовой оценкой альтернативы х по критерию Q_j. Альтернатива с большим значением критериев является в этом смысле этого критерия лучшей. Задача заключается в том, чтобы выбрать рациональную альтернативу по нескольким критериям. Рациональным выбором в этом случае, будет построение множества недоминирующих альтернатив, то есть альтернатив, оптимальных по Парето.

С другой стороны, каждый из критериев описывает обычное отношение преимущества на множестве Х, которое имеет вид: 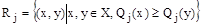. Пусть

.

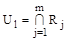В этом случае множество решений, оптимальных по Парето- то есть множество всех недоминирующих альтернатив совпадает с множеством эффективных альтернатив для набора функций, что отображает критерии качества.

Пусть х₀ – недоминирующая альтернатива в множестве (X,U_l), то есть 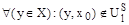, где 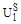- отношение строгого порядка, которое отвечает отношению U_l,

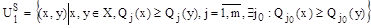
Поэтому для недоминируемых альтернатив справедливо следующее утверждение

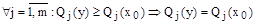
Справедливо и обратное утверждение, то есть любая эффективная альтернатива для критериев 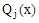, j=1,…,m являются недоминирующими на множестве (X,U_l).

Таким образом для нахождения множества эффективных альтернатив вместо набора отношений R₁,…,R_mможно использовать пересечениеэтих отношений U_l и найти подмножество недоминирующих альтернатив множества (X,U_l).

Пусть

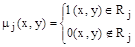
- функция принадлежности множества R_j. В этом случае функция принадлежности пересечения этих отношений будет следующей

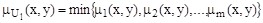
и она эквивалента сворачиванию критериев

.

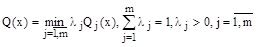Расширяя это определение на класс нечетких отношений, получаем в результате сворачивания первичных нечетких отношений R_j функцию принадлежности нечеткого отношения

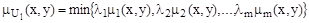
где 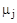-является числом, которое принадлежит интервалу [0,1].В общем случае это отношение не является рефлексивным, то есть не является отношением преимущества в смысле определения, то есть является не удобным для использования при условиях необходимости учета различий в отношении важности первичных нечетких отношений преимущества.

Попробуем обозначить такое отношение, для которого сохронялось бы свойство рефлексивности. С этой целью рассмотрим сворачивание отношений немного другого типа, а именно

.

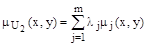Отметим, что результирующее нечеткое отношение в этом случае является рефлексивным, потому что рефлексивными являются состовляющие первичные нечеткие отношения преимуществ R_j. Пусть все первичные нечеткие отношения преимуществ одинаковы по важности, то есть .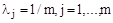

Нечеткое подмножество недоминируемых альтернатив:

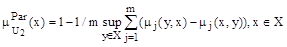
Обозначим 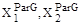- подмножества четко недоминирующих альтернатив множеств 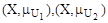которые порождены критериями Q_j(x),j=1,…,m. Для этих подмножеств справедливо соотношение 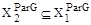. Таким образом в общем случае множество не охватывает все эффективные альтернативы для критериев Q_j(x),j=1,…,m то есть не совпадает с множеством 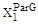. Однако любая произвольная эффективная альтернатива, то есть произвольный элемент 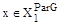, принадлежит множеству 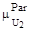с положительной степенью принадлежности, то есть

.

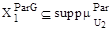Возможно сузить выбор до следующего множества:

.

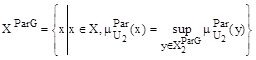Основываясь на предыдущие результаты, приведем алгоритм принятия решений для общей задачи, когда на множестве альтернатив заданы m нечетких отношений преимуществ R₁,…,R_mи весовые коэффициенты 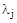относительной важности этих отношений.

1 Строим нечеткое отношение U₁ (пересечение первичных отношений):

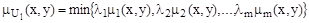
и определяем нечеткое подмножество недоминирующих альтернатив в множестве :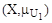

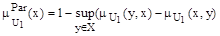
2. Строим нечеткое отношение U2 (сворачивание отношений с сохранением свойств рефлексивности):

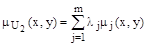
и определяем нечеткое подмножество недоминирующих альтернатив в множестве :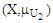

.

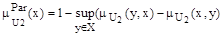3. Находим пересечение множеств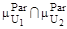

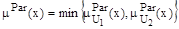
4. Рациональным выбором будет выбор альтернативы из множества:

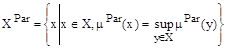
Рациональный выбор на нечетком множестве альтернатив. Пусть Х – универсальное множество альтернатив. На Х задано нечеткое подмножество допустимых альтернатив 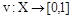. Заданное на Х нечеткое отношение преимущество обозначим как .

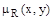Если мы рассмотрим проблему рационального выбора при условии нечеткого множества альтернатив, то необходимо также учитывать следующее отношение преимуществ, которое индуцировано на множестве Х функцией v:

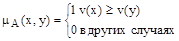
Ввод этого дополнительного отношения преимущества задачу из нечеткого описания множества допустимых альтернатив приводит к задаче с четким множеством альтернатив и дополнительным отношением преимущества, для решения которой можно использовать рассмотренный алгоритм.

Date: 2015-09-20; view: 546; Нарушение авторских прав