Нечеткие отношения преимущества

Проблемы выбора по отношениям преимущества. Пусть Х – некоторое универсальное множество альтернатив, 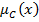- нечеткое описание подмножества допустимых альтернатив при помощи функции принадлежности.

Если любая информация отсутствует, то рациональным считается выбор произвольной альтернативы из множества ,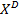

.

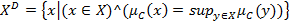В этом случае выбирается альтернатива с наибольшим значением допустимости, потому что нет больше других обоснований для того, чтобы отдать преимущество любой другой альтернативе.

Если в эту модель вводится дополнительная информация, то рациональным может быть выбор из более узкого подмножества множества Х^С.

По результатам опроса выявлено четкое отношение нестрогого преимущества (порядка) R на множестве допустимых альтернатив Х. Это означает, что относительно любой пары альтернатив x,y 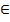X высказано одно из допущений:

1) «x не хуже, чем y», то есть 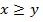или (x,y) 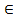R

2) «y не хуже, чем x», то есть y 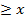или (y,x) 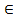R

3) «x и y несравнимы между собой», то есть .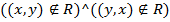

Если существует такая информация, то множество альтернатив может быть сужено путем создания множества не доминирующих альтернатив (множество Парето-оптимальных альтернатив). Выделим соответствующие R отношение строгого преимущества (полного порядка) R^S и отношение безразличия R^I. Для отношения полного порядка выполняется условие 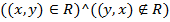. Для обратного R^-1 к R отношения справедливо условие 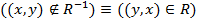. Таким образом отношение строгого преимущества записывается как R^S=R\R^-1. Соответствующее отношение безразличия определяется как отношение, для которого одновременно не выполняется ни 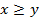, ни y 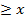или эти два условия одновременно выполняются. Это отношение выполняется, если существующая информация в форме преимуществ недостаточна для того чтобы сделать выбор между x и y.

Отношение R^I можно записать в виде

.

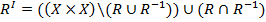Если 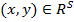, то альтернатива x доминирует над альтернативой y (x>y). Альтернатива х 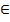Х будет не доминированной, если 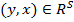для любой альтернативы y 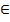Х. Таким образом информация в виде отношения преимущества позволяет сузить класс рациональных выборов до множества не доминируемых альтернатив.

Свойства нечетких отношений преимущества. Нечеткое отношение можно рассматривать как нечеткое подмножество декартового произведения Х 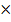Х, поэтому нечеткое отношение преимущества R на множестве Х будем описывать функцией принадлежности 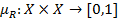, которая имеет свойства рефлексивности.

Нечетким отношением нестрогого преимущества R на заданном множестве альтернатив Х называется произвольно заданное на этом множестве рефлексивное нечеткое отношение. Если 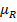- нечеткое отношение нестрогого преимущества, то для любой пары альтернатив значение 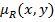интерпретируется как степень выполнения преимущества «х не хуже чем у» или х≥у. Равенство 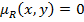означает одно из двух: или 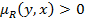, или то что альтернативы несравнимы между собой, то есть 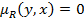. Рефлективность отображает тот факт, что любая альтернатива не хуже самой себя.

По заданному нечеткому отношению R нестрогого преимущества на Х однозначно определяются три следующие отношения: квазиэквивалентности, безразличия и строгого преимущества. Эти отношения определяются по аналогии с соответствующими обычными четкими отношениями, а для получения вида функции принадлежности используются определения операций пересечения, объединения и разницы нечетких множеств.

Нечетким отношением безразличия R^I называется отношение 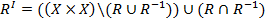с функцией принадлежности ,

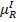Нечетким отношением квазиэквивалентности R^E называется отношение 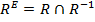c функцией принадлежности ,

.

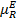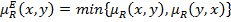По сути, отношение квазиэквивалентности описывает нечеткую эквивалентность, однако термин «отношение эквивалентности» принято использовать к нечетким отношениям, которые являются рефлексивными, симметричными и транзитивными.

Нечеткими отношениями строгого преимущества R^S называются отношения R^S=R\R^-1 с функцией принадлежности ,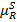

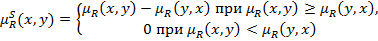
Линейность нечетких отношений. Пусть 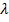- определенное число, которое принадлежит интервалу [0,1]. Нечеткое отношение R с функцией принадлежности 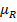называется 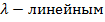, если для его функции принадлежности выполняется условие

.

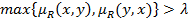Нечеткое отношение R с функцией принадлежности 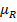называется сильно линейным, если для его функции принадлежности для всех справедливо условие .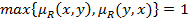

Date: 2015-09-20; view: 488; Нарушение авторских прав