Свойства и условия существования недоминируемых альтернатив

Нечеткое подмножество недоминируемых альтернатив. Пусть Х – множество альтернатив, 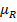– заданное нечеткое отношение преимущества. Нечеткое подмножество недоминируемых альтернатив множества (Х, 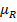), является таким, которое описывается следующей функцией принадлежности :

.

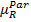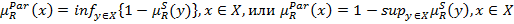Значения 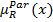является степенью, с которым альтернатива х не доминируется ни одной из альтернатив множества Х. Пусть 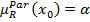для некоторой альтернативе 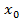. В этом случае может доминировать другими альтернативами, но со степенью, не больше чем 1- 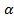. Действительно, при этом

и соответственно, 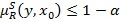для любой альтернативе y .

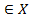Функция принадлежности 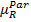нечеткого подмножества недоминирующих альтернатив (Х, 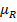) связанная с функцией принадлежности соответственного нечеткого отношения преимущества следующим соотношением:

.

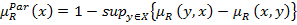Свойства четко недоминируемых альтернатив. Рассмотрим задачу рационального выбора альтернатив в случае, когда для функции принадлежности подмножества недоминируемых альтернатив выполняется условие

.

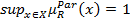В этом случае для каждой альтернативе, которая принадлежит множеству X^Par максимально недоминируемых альтернатив выполняется условие 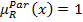, то есть степень недоминирования для каждой такой альтернативе равна единице.

Подмножество четко недоминированных альтернатив X^ParG множества альтернатив Х является множество альтернатив, для которой значение степени недоминированния равна единице, то есть .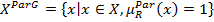

Важным в задачах рационального выбора является вопрос про эквивалентность чисто недоминированных альтернатив. Четко недоминированные альтернативы могут сравниваться лишь в смысле квазиэквивалентности. Если же альтернативы являются не эквивалентными, то для обоснованного выбора приходится использовать дополнительную информацию, внешнюю относительно этой матиматической модели. Если же все четко недоминированные альтернативы эквивалентны одна одной со степенью 1, то дополнительной информации не требуется и рациональным будет выбор произвольного количества.

Эквивалентность альтернатив со значениями, между 0 и 1, степени является промежуточной ситуацией, в которой для обоснованного выбора конкретной альтернативы необходимо использовать меньше дополнительной информации сравнительно со случаем полной неэквивалентности четко недоминированных альтернатив.

,

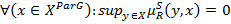где 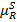- нечеткое отношение строгого преимущества, что отвечает первичному нечеткому отношению преимуществу .

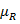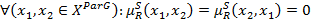
условие которое с учетом определения 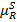эквивалентна 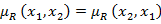, что приводит к соотношению

,

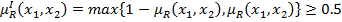то есть любые две четко недоминированные альтернативы связаны отношением безразличия со степенью, больше чем 0,5.

Если для произвольного нечеткого отношения преимущества 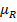выполняется, 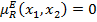при условии, что 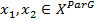(четко недоминированные альтернативы являются неэквивалентными) то в этом случае 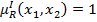, то есть 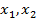являются полностью несравнимыми между собой.

Однако это может не выполнятся, если 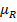линейное.

Если 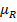является 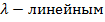и 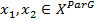то учитывая определение 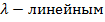получаем, что 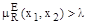, то есть при этом условии любые четкие недоминирующие альтернативы являются эквивалентными со степенью большей чем 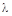.В частных случаях при слабо линейном нечетком отношении преимущество 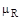любые две четко недоминированные альтернативы являются эквивалентными с положительным значением степени принадлежности.

Рассмотрим следующую величину:

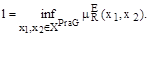
Значение этой величины можно рассматривать как меру количества существующей в задаче информации, которая необходима для однозначного выбора альтернативы. Ее так же можем считать и мерой линейности нечеткого отношения преимущества 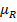, поскольку для сильно линейного отношения ее значение является максимальным, то есть равно 1.

Если нечеткое отношение преимущества является сильно линейным, и 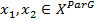то следствием из определения сильной линейности является равенство 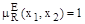, то есть произвольные четко недоминированные альтернативы в этом случае являются определенно эквивалентными, то есть обоснованным является выбор любой из них. Таким образом сильно линейное нечеткое отношение преимущества, такое что во множестве (Х, 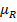) присутствуют чисто недоминирующие альтернативы, имеет в себе всю необходимую информацию для принятия решений.

Если 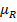- сильно линейное нечеткое отношение преимущества во множестве Х, то для любой альтернативы 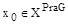равенство 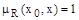выполняется так же и для любой альтернативы 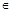х Х.

Если 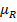- сильно линейное транзитивное нечеткое отношение преимущества во множестве Х, и 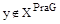то для любой альтернативы х 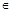Х выполняется условие .

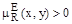Если нечеткое отношение преимущества 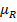на множестве Х является сильно линейным и транзитивным, 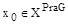и для некоторой альтернативы х 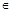Х выполняются условия 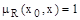, то .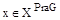

Условия существования четко недоминируемых альтернатив. Пара 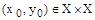называется седловой точкой функции (максимум за х, минимум за у), если для любых 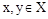выполнены следующие неравенства

.

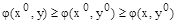Функция называется антисимметричной, если для любых 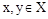выполняется равенство .

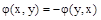Если 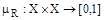- нечеткое отношение преимущества на множестве альтернатив Х, то является чисто недоминированной альтернативой на множестве 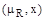лишь тогда, когда пара 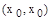является седловой точкой функции 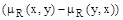на множестве .

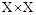Элементы 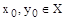являются четко недоминированными альтернативами на множестве 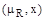лишь тогда, когда пара 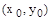- седловая точка функции 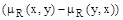на множестве .

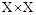Таким образом любые условия, достаточные для существования седловой точки функции 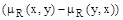на множестве 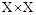, являются достаточными и для существования четко недоминируемых альтернатив во множестве .

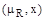В конечном множестве Х с заданным на нем транзитивным нечетким отношением преимущество 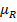существует как минимум одна четко недоминируемая альтернатива.

Date: 2015-09-20; view: 456; Нарушение авторских прав