Аналитический метод решения игры типа 2 х 2

Рассмотрим игру без седловой точки типа 2 х 2 с платежной матрицей

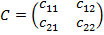
и найдем оптимальную стратегию

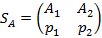
игрока А. Согласно следствию 3 из основной теоремы теории игр эта стратегия обеспечивает игроку А выигрыш, равный цене игры V, даже если игрок В не выходит за пределы своих полезных стратегий. В данной игре обе чистые стратегии игрока В являются полезными, поскольку в противном случае игра имела бы решение в области чистых стратегий, т.е. была бы игрой с седловой точкой.

Отсюда вытекает, что неизвестные 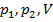удовлетворяют следующей системе из трех линейных уравнений

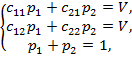
решение которой имеет вид

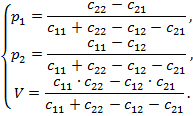
Аналогичным образом можно найти оптимальную стратегию

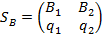
игрока В. В этом случае неизвестные 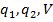удовлетворяют системе уравнений

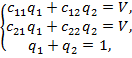
решение которой имеет вид

Применим теперь полученные формулы к карточной игре типа «веришь – не веришь».

Пример 6.1. Имеются две карты: туз и двойка. Игрок А наугад берет одну из них. Если А взял туза, то он заявляет: «У меня туз» и требует от противника рубль. Если же А взял двойку, то он может либо сказать: «У меня туз» и потребовать рубль, либо признаться, что у него двойка и заплатить рубль. Игрок В, если ему предлагают рубль, берет его. Однако, если у него требуют рубль, то В может либо поверить, что у А туз, и заплатить рубль, либо не верить и потребовать проверки. Если в результате проверки окажется, что у А действительно туз, то В платит 2 рубля. Если же выяснится, что у А была двойка, то А платит 2 рубля.

Найти оптимальные стратегии для каждого из игроков.

Решение. У игрока А есть 2 стратегии: А ₁ – обманывать, А ₂ – не обманывать. У игрока В тоже есть 2 стратегии: В ₁ – верить, В ₂ – не верить. Это позволяет найти все элементы платежной матрицы игры, вычислив средний выигрыш для каждой комбинации стратегий.

1. А ₁ В ₁ (А обманывает, В верит).

Если А берет туза (вероятность этого 0,5), то он требует рубль. В верит ему и платит. Если А берет двойку (вероятность этого также 0,5), то он обманывает и тоже требует рубль. В верит ему и платит. Средний выигрыш А равен .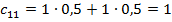

2. Комбинация А ₁ В ₂ (А обманывает, В не верит).

Если А берет туза, то он требует рубль, а В не верит и после проверки платит 2 рубля. Если же А взял двойку, то он обманывает и тоже требует рубль. В не верит ему, и в результате А платит 2 рубля. Средний выигрыш А равен .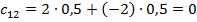

3. Комбинация А ₂ В ₁ (А не обманывает, В верит).

Если А берет туза, то он требует рубль, В платит 1 рубль. Если А берет двойку, то он сообщает об этом и платит рубль. Средний выигрыш А равен .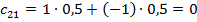

4. Комбинация А ₂ В ₂ (А не обманывает, В не верит).

Если А берет туза, то он требует рубль, В проверяет и платит 2 рубля. Если А берет двойку, то он сообщает об этом и платит рубль. Средний выигрыш А равен .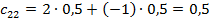

Отсюда вытекает, что платежная матрица имеет вид

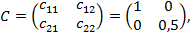
и можно найти нижнюю и верхнюю цены игры:

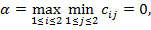
Следовательно, игра не имеет седловой точки, и ее решение нужно искать в области смешанных стратегий. Для этого воспользуемся формулами полученными выше:

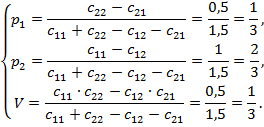
Следовательно, смешанная стратегия игрока А имеет вид

.

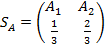Далее получаем

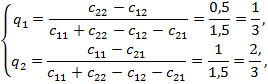
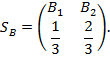
Таким образом, оптимальным для А будет в одной трети случаев обманывать, а в двух третях случаев – не обманывать. Такая тактика обеспечит ему средний выигрыш, равный V =1/3. Если бы А стал пользоваться своей максиминной стратегией, то его выигрыш был бы равен .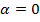

Для В оптимальная стратегия – это в одной трети случаев верить А и платить ему рубль, а в остальных случаях требовать проверки. В этой ситуации его средний проигрыш составит 1/3, тогда как при применении минимаксной стратегии он будет проигрывать в среднем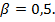

Значение V =1/3 показывает, что рассмотренная игра выгодна для А и невыгодна для В, поскольку, пользуясь своей оптимальной стратегией, А всегда может обеспечить себе положительный средний выигрыш.

7. Графический метод решения игр типа 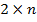и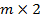

Рассмотрим игру типа 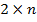с платежной матрицей

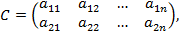
и проведем через точку (1;0) координатной плоскости Oxy прямую l, перпендикулярно оси абсцисс. После этого для каждой из стратегий B_i (i=1,2,…,n) проведем прямую

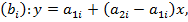
соединяющую точку 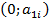на оси Oy с точкой на прямой l. Ось Oy отвечает за стратегию А ₁, а прямая l – за стратегию А ₂.

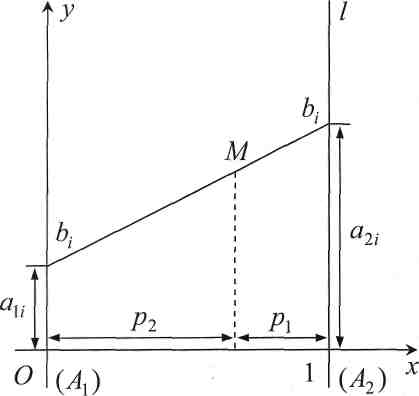
Если игрок А применяет смешанную стратегию

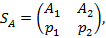
то его выигрыш в случае, если противник применяет чистую стратегию В_i, равен

и этому выигрышу соответствует М на прямой b_i с абсциссой x=p₂.

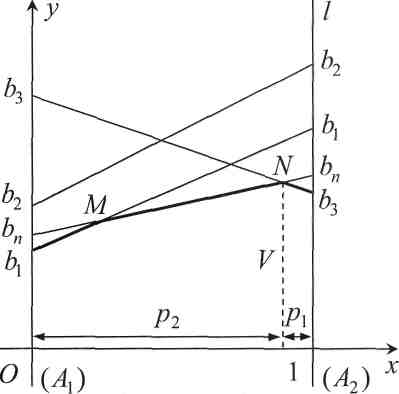
Ломанная b₁MNb ₃, отмеченная на чертеже жирной линией, позволяет определить минимальный выигрыш игрока А при любом поведении игрока В. Точка N, в которой эта ломанная достигает максимума, определяет решение и цену игры. Ордината точки N равна цене игры V, а ее абсцисса p ₂ – частоте применения стратегии A ₁ в оптимальной смешанной стратегии игрока А.

Далее непосредственно по чертежу находим пару «полезных» стратегий игрока В, пересекающихся в точке N (если в точке N пересекается более двух стратегий, то выберем любые две из них). Пусть это будут стратегии B_i и B_j. Поскольку выигрыш игрока А, если он придерживается оптимальной стратегии, не зависит от того, в каких пропорциях игрок В применяет эти стратегии, то неизвестные p ₁, p ₂, V определяются из системы уравнений

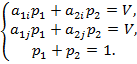
Частоты q₁, q₂ в оптимальной стратегии

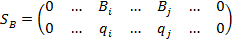
игрока В определяются из соотношения

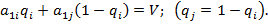
Замечание. Иногда точка N не является пересечением двух стратегий, а попадает на одну из прямых х =0 или х =1. В этом случае решением игры будут соответствующие чистые стратегии.

Для игры 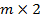решение находится совершенно аналогично. Действительно, поскольку выигрыш игрока А одновременно является проигрышем игрока В, то для решения задачи нужно построить ломанную, соответствующую верхней границе выигрыша игрока А, а затем найти на ней точку с минимальной ординатой.

Пример 7.1. Пусть игра задана матрицей

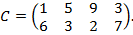
Найти оптимальные стратегии игроков и определить цену игры.

Date: 2015-09-20; view: 4644; Нарушение авторских прав