Игры, повторяемые многократно. Смешанные стратегии

Если партнеры играют только один раз, то игрокам целесообразно придерживаться принципа минимакса, как в игре с седловой точкой, так и в игре без седловой точки.

В случае многократного повторения игры с седловой точкой игрокам также целесообразно придерживаться принципа минимакса.

Если же многократно повторяется игра без седловой точки, то постоянное использование минимаксных стратегий становится невыгодным.

Действительно, в игре без седловой точки элемент платежной матрицы 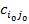, соответствующий минимаксной стратегии игрока А, не обязан быть минимальным в своей строке. Следовательно, игрок В, зная о том, что игрок А в следующей игре будет использовать минимаксную стратегию 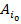, может выбрать стратегию, отвечающую минимальному элементу строки . В результате выигрыш игрока А уменьшится от величины 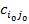, до величины 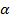. Аналогично может поступить и игрок А, неожиданно применив против игрока В стратегию, соответствующую максимальному элементу столбца .

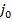Более того, доказано, что при многократно повторяемой игре без седловой точки игроку А, для обеспечения среднего выигрыша, большего, чем 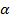, следует чередовать свои стратегии 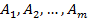. Игроку В для улучшения результата также целесообразно чередовать свои стратегии .

По этой причине для многократно повторяемых игр без седловой точки вводится следующее определение.

· В играх, которые повторяются многократно, каждая из стратегий 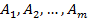называется чистой стратегией.

· Стратегия игрока А, обозначаемая

и состоящая в том, чтобы применять чистые стратегии 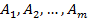, чередуя их по случайному закону с частотами 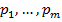, называется смешанной стратегией. Частоты 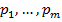удовлетворяют соотношению

.

· Чистые и смешанные стратегии игрока В определяются аналогично.

Замечание. Каждая чистая стратегия является частным случаем смешанной стратегии, когда одна из стратегий применяется с частотой 1, а все остальные – с частотой 0.

· Смешанные стратегии, избранные игроками, называются оптимальными, если одностороннее отклонение любым игроком от своей оптимальной стратегии может изменить средний выигрыш только в сторону, невыгодную для этого игрока.

· Совокупность, состоящая из оптимальной стратегии одного игрока и оптимальной стратегии другого игрока, называется решением игры.

· Средний выигрыш V при применении обоими игроками оптимальных стратегий называется ценой игры.

· Стратегии, входящие с ненулевыми частотами в оптимальную стратегию игрока, называются полезными.

В 1928 году фон Нейманом была доказана основная теорема теории игр, утверждающая, что каждая игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий.

Поскольку все чистые стратегии являются частными случаями смешанных стратегий, то из основной теоремы теории игр можно получить

Следствие 1. Любая игра имеет цену.

Следствие 2. Цена игры удовлетворяет неравенству .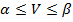

Следствие 3. Средний выигрыш остается равным цене игры, если один из игроков придерживается своей оптимальной стратегии, а другой игрок применяет свои полезные стратегии с любыми частотами.

Date: 2015-09-20; view: 1524; Нарушение авторских прав