Математико-географическое моделирование

Математическое моделирование геосистем, проводимое на уровне объектов и отношений между ними, связано с созданием логико-математических конструкций, отображающих количественные отношения реальных географических объектов. Процесс построения моделей ведётся по принципам математического моделирования на базе системного подхода с учётом специфики географического объекта. Получаемые при этом логико-математические последовательности величин, характеризующие состояние геосистем, образуют особые математико-географические модели, а сам процесс их создания и последующее получение по ним результатов носит название математико-географического моделирования (МГМ). В этом случае вторичным предметом исследования становятся логико-математические символы и их последовательности – формулы, уравнения и т. п., описывающие релевантные географические признаки оригинала. При МГМ привлекаются различные средства математического аппарата: теория вероятности, теория оптимальных процессов, теория множеств, эффективно используются методы математической физики, корреляционного анализа, счётные методы и др.

Математико-географические модели могут предназначаться для исследования разных сторон народного хозяйства (в частности, его производственно-технологической, социальной, территориальной структур) и его отдельных частей. При классификации моделей по исследуемым процессам и содержательной проблематике можно выделить модели народного хозяйства в целом и его подсистем отраслей, регионов и т. д., комплексы моделей производства, потребления, формирования и распределения доходов, трудовых ресурсов и пр.

Математико-географическое моделирование – сложный процесс, включающий ряд последовательных этапов (рис. 2).

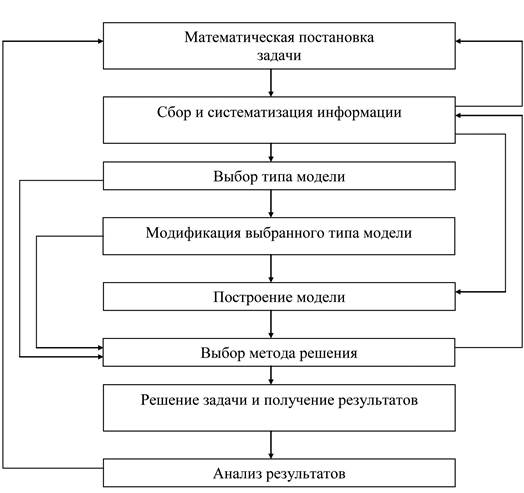
Рис. 2. Схема математико-географического моделирования [6]

На первом подготовительном этапе ставится цель, и определяются задачи исследования. Этот этап включает выделение важнейших черт и свойств моделируемого объекта и абстрагирование от второстепенных; изучение структуры объекта и основных зависимостей, связывающих его элементы; формулирование гипотез (хотя бы предварительных), объясняющих поведение и развитие объекта.

Второй этап включает согласование задач исследования, установление логической последовательности их решения и подготовка исходной информации. Моделирование предъявляет жёсткие требования к системе информации. В то же время реальные возможности получения информации ограничивают выбор моделей, предназначаемых для практического использования. При этом принимается во внимание не только принципиальная возможность подготовки информации (за определённые сроки), но и затраты на подготовку соответствующих информационных массивов. Эти затраты не должны превышать эффект от использования дополнительной информации. В процессе подготовки информации широко используются методы теории вероятностей, теоретической и математической статистики.

На третьем этапе осуществляется построение математической модели. Это этап формализации географической проблемы, выражения её в виде конкретных математических зависимостей и отношений (функций, уравнений, неравенств и т. д.). Обычно сначала определяется основная конструкция (тип) математической модели, а затем уточняются детали этой конструкции (конкретный перечень переменных и параметров, форма связей).

Построение модели подразделяется в свою очередь на несколько стадий. Неправильно полагать, что чем больше фактов учитывает модель, тем она лучше «работает» и даёт лучшие результаты. То же можно сказать о таких характеристиках сложности модели, как используемые формы математических зависимостей (линейные и нелинейные), учёт факторов случайности и неопределённости и т. д. Излишняя сложность и громоздкость модели затрудняют процесс исследования. Нужно учитывать не только реальные возможности информационного и математического обеспечения, но и сопоставлять затраты на моделирование с получаемым эффектом (при возрастании сложности модели прирост затрат может превысить прирост эффекта).

После построения модели выясняются её общие свойства. Здесь применяются чисто математические приёмы исследования. Наиболее важный момент – доказательство существования решений в сформулированной модели (теорема существования). Если удастся доказать, что математическая задача не имеет решения, то необходимость в последующей работе по первоначальному варианту модели отпадает; следует скорректировать либо постановку экономической задачи, либо способы её математической формализации.

Следующий этап включает разработку алгоритмов для численного решения задачи, составления программ на ЭВМ и непосредственное проведение расчётов. Трудности этого этапа обусловлены, прежде всего, большой размерностью географических задач, необходимостью обработки значительных массивов информации. Обычно расчёты по математико-географической модели носят многовариантный характер. Благодаря высокому быстродействию современных компьютеров удаётся проводить многочисленные «модельные» эксперименты, изучая «поведение» модели при различных изменениях некоторых условий. Исследование, проводимое численными методами, может существенно дополнить результаты аналитического исследования, а для многих моделей оно является единственно осуществимым. Класс географических задач, которые можно решать численными методами, значительно шире, чем класс задач, доступных аналитическому исследованию.

На заключительном этапе (анализ результатов) встает вопрос об адекватности полученных данных реальному объекту и о степени практической применимости последних. Математические методы проверки могут выявлять некорректные построения модели и тем самым сужать класс потенциально правильных моделей. Неформальный анализ теоретических выводов и численных результатов, получаемых посредством модели, сопоставление их с имеющимися знаниями и фактами действительности также позволяют обнаруживать недостатки постановки экономической задачи, сконструированной математической модели, её информационного и математического обеспечения.

Наиболее широкое распространение в географии получили многомерные математические модели, применяемые для типологии. Они подразделяются на две большие группы: первые строятся при условии гомогенности территориальных единиц внутри иерархически упорядоченных таксонов; вторые учитывают гомогенность объединяемых в одну группу таксономических единиц [5].

Одним из наиболее перспективных методов моделирования геосистем и процессов, протекающих в них, является имитационное моделирование. По словам известного в этой области учёного P. Шеннона, «идея имитационного моделирования проста и интуитивно привлекательна, позволяет экспериментировать с системами, когда на реальном объекте этого сделать нельзя» [8, с. 7]. В основе этого метода теория вычислительных систем, статистика, теория вероятностей, математика.

Имитационное моделирование представляет собой формализацию эмпирических знаний о рассматриваемом объекте с использованием современных компьютеров. Большинство имитационных моделей построены по типу «чёрного ящика», т. е. сама система (её элементы, структура) представлены в виде «чёрного ящика»: есть какой-то вход в него, который описывается экзогенными переменными (возникают вне системы, под воздействием внешних причин), и выход (описывается выходными переменными), который характеризует результат действия системы.

В имитационном исследовании большое значение имеет этап оценки модели, который включает в себя следующие шаги:

1) верификация модели (модель ведёт себя так, как это было задумано исследователем);

2) оценка адекватности (проверка соответствия модели реальной системе);

3) проблемный анализ (формирование статистически значимых выводов на основе данных, полученных в результате экспериментов с моделью).

Большой интерес в имитационном моделировании представляет метод системной динамики, разработанный одним из крупнейших специалистов в области теории управления, профессором Джеем Фоppестеpом. Его первая книга в этой области – «Кибернетика предприятия» – вызвала огромный интерес мировой науки к методу системной динамики в имитационном моделировании.

Начало глобальному моделированию положил другой труд Дж. Фоppестеpа «Мировая динамика» [7]. Здесь он рассматривает мир как единое целое, как единую систему различных взаимодействующих процессов: демографических, промышленных, процессов исчерпания природных ресурсов и загрязнения окружающей среды, процесса производства продуктов питания.

Имитационные эксперименты состоят из многократных расчётов по заданной модели при изменении входных параметров и предполагают целенаправленный поиск оптимальных решений, в частности касающихся рациональности взаимодействия природных и хозяйственных геосистем. Использование этих моделей позволяет качественно и количественно оценить варианты их функционирования при различных уровнях антропогенного воздействия с учётом естественной способности к самоочищению и самовосстановлению.

Область применения методов математического моделирования в географии непрерывно расширяется. Однако абсолютное большинство мо­делей основаны на линейных зависимостях между компонентами систем и между системами, что часто не позволяет описать даже самые существенные свойства исследуемого объекта. Эти методы оказываются неэффективными при моделировании сложных систем, изучение которых основано на использовании больших массивов данных при наличии аномалий пространственных и временных параметров. Для того, чтобы избежать эти недостатки при разработке моделей, необходимо использовать новые методы математического моделирования, существующие в точных науках. Для выявления свойств и пространственно-временных закономерностей функционирования территориальных систем перспективно применение новых для географических исследований математических методов: интег­ро-дифференциальных уравнений Фредгольма и Вольтера, сплайн-функций, функций Грина, структурной и параметрической идентификации, спектрального анализа, которые позволяют более точно описать сложные геосистемы на основе учёта разнообразных природных и социально-экономических факторов территориальной дифференциации геосистем. Данные методы моделирования развития территориальных систем позволяют дать более содержатель­ную интерпретацию в условиях неопределённости среды и осуществить целенаправленный поиск устойчивого состояния и структуры геосистем в зависимости от степени антропогенной нагрузки и различной способ­ности природных систем к самовосстановлению. Некоторые из этих методов использованы нами для решения ряда задач социально-экономической географии [2; 3].

Таким образом, накопленный в науке опыт системных исследований и моделирования создаёт благоприятные предпосылки для решения широкого круга вопросов, связанных с изучением территориальных систем, их взаимодействия друг с другом и окружающей средой, рационального использования природного потенциала территории.

Литература

1. Модели в географии: пер. с англ. / под. ред. Дж Р. Чорли, П. Хаггета. М.: Прогресс, 1971. 384 с.

2. Носонов А. М. Моделирование экономических и инновационных циклов в сельском хозяйстве // Национальные интересы: приоритеты и безопасность, 2014. № 1 (238). С. 24–33.

3. Носонов А. М. Территориальные системы сельского хозяйства (экономико-географические аспекты исследования). М.: Янус-К, 2001. 324 с.

4. Охрана ландшафтов. Толковый словарь / под. ред. В. С. Преображенского. М.: Прогресс, 1982. 272 с.

5. Тикунов В. С. Классификации в географии: ренессанс или увядание? (Опыт формальных классификаций). М.–Смоленск: Изд-во СГУ, 1997. 367 с.

6. Трофимов А. М., Игонин Е. И. Концептуальные основы моделирования в географии (Развитие основных идей и путей математизации и формализации в географии). Казань: Изд-во «Матбугат йорты», 2001. 340 с.

7. Форрестер Д. Мировая динамика. М.: АСТ, 2006. 384 с.

8. Шеннон Р. Имитационное моделирование систем – искусство и наука. М.: Мир, 1978. 418 с.

Date: 2015-09-20; view: 3973; Нарушение авторских прав