
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Мет 3082,2
|
|
оЧю - Ъ - дг* = ТТЙГ1000 = 2740'2,
Динамика средств на персональном счете и резерва характеризуется следующими данными.
| x + t | |||||
| 2740 2740 | 4216 4579 | 6486 7919 | 4582 7120 |
Полностью сумма на персональном счете будет исчерпана спустя 10 лет после начала выплат пенсии. Теоретическая нехватка средств на индивидуальном счете застрахованного компенсируется, как и в предыдущем примере, за счет действия принципа солидарности застрахованных.
Динамика резерва в рассматриваемом виде страхования различается по периодам. В первом, до начала выплаты пенсии, она описывается формулой (17.23). Что касается второго, то здесь искомая зависимость более сложная. Найдем соотношение двух последовательных показателей резерва:
| V N Н-1 Yx _ nx+t+\ V ~~ П t у х ^jc+z+I | nx+t _ nx+t+\ "x+t "x+t | x------- Px+t |
| Таким образом, | ||
| "x+t+\ |
| f+l rx r x |
Nx+t x Px+t
(1 + 0.
(17.30)
Очевидно, что, если второй сомножитель в правой части равенства (17.30) меньше множителя наращения (1 +0» то резерв уменьшается с каждым шагом во времени.
ПРИМЕР17.12. Продолжим пример 17.11. Найдем величину резерва для мужчины в возрасте 61 год, применив формулу (17.30):
Чл 2693
11^50 = lo^so х Т;-------------- х 1.09 = 7919 х———ГТГГГ-х 1,09 =
и 50 ю 50 Л/gQ х р61 3082 х 0,9692
= 7781, что меньше резерва для 60 лет (см. пример 17.10).
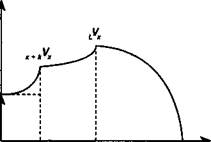
Ничего принципиально не меняется, если взнос производится не разовым платежом, а в рассрочку. Пусть предусматривается пожизненная выплата пенсий и рассрочка взносов в течение к лет. Изменение резерва во времени изображено на рис. 17.6. Общий срок действия страхового полиса в этом случае можно разбить на три периода. В первом, в возрасте от х до х + к, осуществляются взносы и происходит ускоренное накопление, во втором, от х + к и до возраста L, сумма резерва увеличивается только за счет процентов, в третьем средства расходуются на выплату пенсий, причем на остаток средств начисляются проценты. В "финальном" возрасте со после выплаты пенсии резерв равен нулю. Аналогичное можно сказать и относительно динамики средств на персональном счете, кроме момента полного исчерпания средств, который происходит в возрасте (А < ш).
|
Резерв
Р*
х x-i-fr L о Возраст
Рис 17.6
Ограничимся случаем, когда пенсии и взносы выплачиваются раз в году пренумерандо и не учитывается дополнительный инвестиционный доход, выплата которого предусматривается в некоторых пенсионных фондах. Запишем в общем виде формулу величины резерва в момент х + г.
где Ax¥t — современная стоимость пенсионных выплат, производимых после возраста х + /, ax^t — стоимость немедленного ограниченного страхового аннуитета пренумерандо в возрасте х + / лет, Рх — годовой размер премии, установленный в возрасте х лет.
Формула (17.31), как видим, предполагает определение будущих (ожидаемых) поступлений. Ее результат представляет собой "чистые" обязательства страховщика перед участником в возрасте х + / лет. Подобный способ получил название прямой метод определения резерва.
Определим резерв для случая, когда пенсия пожизненная, R = 1, нетто-премия равна Рх в расчете на денежную единицу пенсии, пенсия и премии выплачиваются пренумерандо. В этом случае для первого периода (/ < к) находим
/ К * n-t\dx ~ Рх х йх:Щ> <17-32)
где п = L — х — временной интервал от х до L лет, ^^ах — стоимость отложенного пожизненного страхового аннуитета пренумерандо, dx.jzji — стоимость немедленного ограниченного аннуитета.
Величина Рх находится на основе принципа эквивалентности обязательств страховщика и страхователя. Если R = 1, то из равенства этих обязательств следует, что 0VX= 0 и нетто-пре-мия находится как соотношение двух страховых аннуитетов — отложенного пожизненного и немедленного ограниченного, а именно:
Date: 2015-09-19; view: 394; Нарушение авторских прав