
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Математическое приложение к главе. Доказательство формулы (7.12)
|
|
Доказательство формулы (7.12)
Найдем барьерную точку выпуска для условия, согласно которому современная стоимость доходов равна современной стоимости затрат. При расчете современных стоимостей полагаем, что выпуск и реализация продукции равномерно распределены в пределах года. В связи с этим без заметной потери точности в расчетах отнесем эти величины к серединам соответствующих лет. В терминах финансовой математики соответствующие потоки представляют собой постоянные годовые ренты с платежами в середине периодов (см. § 6.3). Пусть PV— оператор определения современной стоимости соответствующего потока платежей. Современная стоимость потока переменных и постоянных затрат, в которые включены и амортизационные начисления, в этом случае составит:
PV(f+ d+ cQ) = (/•+ d + cQ)v05 +... +
(1) + (/> d + cQ)v^5 = (/•+ d + cQ)an;i (1 + /)4
где апЛ — коэффициент приведения постоянной ренты, v — дисконтный множитель.
В свою очередь современная стоимость поступлений находится как
PV(pQ) = pQv0*5 + pQv15 +... + pQv"-^ =
(2)
= />e%(i + o0'5.
Из равенства
(/•+ d + cQk)an;i (1 + if* = PQkan;i(\ + О0'5 следует искомая формула
* /? — с
Глава 8 РИСК И ДИВЕРСИФИКАЦИЯ
Риск
В финансовом анализе производственных инвестиций мы неизбежно сталкиваемся с неопределенностью, неоднозначностью показателей затрат и отдачи. В связи с этим возникает проблема измерения риска и его влияния на результаты инвестиций. Поскольку вопросы, связанные с измерением риска в экономической деятельности, рассмотрены в отечественной литературе явно недостаточно, остановимся на них более подробно, чем, возможно, это необходимо для раскрытия основной темы данной работы.
Широко распространенный термин "риск", как известно, понимается неоднозначно. Его содержание определяется той конкретной задачей, где этот термин используется. Достаточно просто перечислить такие понятия как кредитный, валютный, инвестиционный, политический, технологический риски, риск ликвидности активов и т.д. Отметим, что даже самое общее определение этого понятия не оставалось неизменным во времени. Говоря о первом в экономике научном определении риска, обычно ссылаются на Ф. Найта (1921), который предложил различать риск и неопределенность. Риск имеет место тогда, когда некоторое действие может привести к нескольким взаимоисключающим исходам с известным распределением их вероятностей. Если же такое распределение неизвестно, то соответствующая ситуация рассматривается как неопределенность. Как нам представляется, здесь речь идет, скорее, не об определении риска, а лишь о наличии информации, характеризующей риск.
В экономической практике, особенно финансовой, обычно не делают различия между риском и неопределенностью. Чаще всего под риском понимают некоторую возможную потерю, вызванную наступлением случайных неблагоприятных событий. В некоторых областях экономической деятельности сложились
устойчивые традиции понимания и измерения риска. Наибольшее внимание к измерению риска проявлено в страховании. Объяснять причину такого внимания нет необходимости. Измеритель риска, как возможная потеря страховщика, был использован еще в конце XVIII в. В других направлениях финансовой деятельности под риском также понимается некоторая потеря. Она может быть объективной, т.е. определяться внешними воздействиями на ход и результаты деятельности хозяйствующего субъекта. Так, например, потеря покупательной способности денег (инфляционный риск) не зависит от воли и действий их владельца. Однако, часто риск, как возможная потеря, может быть связан с выбором того или иного решения, той или иной линии поведения. Заметим также, что в некоторых областях деятельности риск понимается как вероятность наступления некоторого неблагоприятного события. Чем выше эта вероятность, тем больше риск. Такое понимание риска оправданно в тех случаях, когда событие может наступить или не наступить (банкротство, крушение и т.д.).
Когда невозможны непосредственные измерения размеров потерь или их вероятностей, риск можно квантифицировать с помощью ранжирования соответствующих объектов, процессов или явлений в отношении возможного ущерба, потерь и т.д. Ранжирование обычно основывается на экспертных суждениях.
Естественной реакцией на наличие риска в финансовой деятельности является стремление компенсировать его с помощью так называемых рисковых премий (risk premium), которые представляют собой различного рода надбавки (к цене, уровню процентной ставки, тарифу и т.д.), выступающие в виде "платы за риск". Второй путь ослабления влияния риска заключается в управлении риском. Последнее осуществляется на основе различных приемов, например, с помощью заключения форвардных контрактов, покупки валютных или процентных опционов и т.д.
Одним из приемов сокращения риска, применяемым в инвестиционных решениях, является диверсификация, под которой понимается распределение общей инвестиционной суммы между несколькими объектами. Диверсификация — общепринятое средство сокращения любого вида риска. С увеличением числа элементов набора (портфеля) уменьшается общий размер риска. Однако только в случае, когда риск может быть измерен и представлен в виде статистического показателя, управление риском получает надежное основание, а последствия диверсифи-
кации поддаются анализу с привлечением методов математической статистики.
В инвестиционном анализе и страховом деле риск часто измеряется с помощью таких стандартных статистических характеристик, как дисперсия и среднее квадратическое (стандартное) отклонение. Обе характеристики измеряют колебания, в данном случае — колебания дохода. Чем они больше, тем выше рассеяние показателей дохода вокруг средней и, следовательно, степень риска.
Напомним, что между дисперсией (D) и средним квадрати-ческим отклонением (а) существует следующее соотношение:
а» V/>.
В свою очередь дисперсия относительно выборочной средней (х) находится как
п - 1
где п — количество наблюдений, х — средняя случайной переменной х.
|
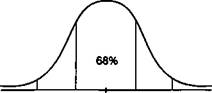
| -2а -а х +а +2а |
| Рис. 8.1 |
Как известно, среднее квадратическое отклонение имеет то неоспоримое достоинство, что при близости наблюдаемого распределения (например, распределении дохода от инвестиций) к нормальному, что, строго говоря, должно быть статистически проверено, этот параметр может быть использован для определения границ, в которых с заданной вероятностью следует ожидать значение случайной переменной. Так, например, с вероятностью 68% можно утверждать, что значение случайной переменной х (в нашем случае доход) находится в границах х ± a, a с вероятностью 95% — в пределах х ± 2а и т.д. Сказанное иллюстрируется на рис. 8.1
Date: 2015-09-19; view: 472; Нарушение авторских прав