Основні поняття та визначення

Нехай на відрізку [а; b] визначено певний клас функцій {Р(х)}, наприклад клас алгебраїчних многочленів, а в точках х₀, х₁,..., х_n цього проміжку задано значення деякої функції y=f(x): y₀=f(x₀), y₁=f(x₁),….y_n=f(x_n).

Інтерполяція – це наближена заміна функції f на відрізку [а; b] однією з функцій Р(х) цього класу так, щоб функція P(х) в точках x₀,x₁,..., x_n набувала тих самих значень, що й функція f, тобто щоб Р(x_i)= у_i (і = 0, 1,..., n). На Рис.1.1.1 зображена інтерполяція функції.

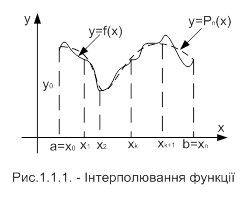
Вузли інтерполювання – це точки х₀, х_i,..., х_n, в яких задана функція.

Функція Р(х) називається інтерполюючою функцією.

Інтерполяційна формула – це формула у=P(х), за допомогою якої обчислюють значення функції f у проміжку [а;b].

Якщо функція Р(х) належить класу алгебраїчних многочленів, то інтерполювання називається параболічним. Параболічне інтерполювання найзручніше, оскільки многочлени, які прості за формою і не мають особливих точок, можуть набувати довільних значень, їх легко обчислювати, диференціювати й інтегрувати.

Інтерполяційний многочлен – це многочлен виду Р_n(х), який задовольняє умови 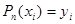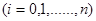, наближену рівність f(x)=P_n(x) називають інтерполяційною формулою, а різницю R_n(f,x)=f(x) – P_n(x) — залишковим членом інтерполяційної формули. Хоч інтерполяційний многочлен і єдиний, проте можливі різні форми його запису. Інтерполяційний поліном має слідуючий вид:

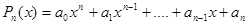( 1.1)

При обробці результатів вимірювань часто виникає необхідність побудови емпіричної формули, більш простішої, чим інтерполяційний поліном, яка б добре відображала фізичні властивості досліджуваного процесу.

В цьому випадку необхідно рішити задачу відшукання оптимальних в деякому випадку оцінок параметрів системи.

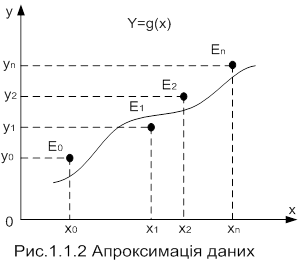
Апроксимація – це наближений опис однією функцією (апроксимувальною) заданого вигляду іншої функції (апроксимовної), яка задається у будь-якому вигляді (при апроксимації даних вона задається у вигляді масивів даних).

Нехай у таблиці задан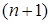а точка 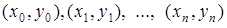і треба знайти апроксимувальну криву 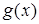в діапазоні 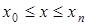(рисунок 1.1.2.). В цьому випадку похибка в кожній табличній точці буде 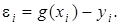Тоді сума квадратів похибок визначається виразом:

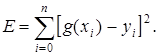(1.2)

Як правило, функцію 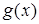обирають у вигляді лінійної комбінації вибраних функцій :

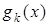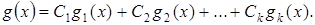(1.3)

Умова мінімуму Е визначається рівнянням:

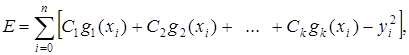(1.4)

Вибір функції 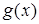повинен здійснюватися з урахуванням характеру табличних даних (періодичності, властивості симетрії, існування асимптотики та т. п.). Іноді таблицю розбивають на декілька частин та добирають окрему апроксимувальну криву для кожної частини. Такий підхід задовольняє ті випадки, коли дані відповідають різним фізичним станам системи.

Залишкова середня квадратична похибка апроксимації оцінюється:

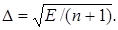(1.5)

При побудові апроксимувальної функції використовуються ортогональні поліноми, для яких

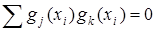, якщо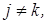

Коефіцієнти визначаються зі співвідношень

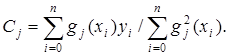(1.6)

Це спрощує задачу, і тому в багатьох стандартних програмах припасування кривих використовують ортогональні поліноми.

Date: 2015-09-18; view: 420; Нарушение авторских прав