
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Доказательство
|
|
Заметим, что так как по условию теоремы множество планов P’ не пусто, то согласно теореме 1.4 оно имеет хотя бы одну крайнюю точку.
Рассмотрим 2 случая:
1. Пусть Р’ – выпуклый многогранник, а 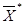 - решение задачи линейного программирования. Тогда согласно теореме, которая гласит, что любая точка
- решение задачи линейного программирования. Тогда согласно теореме, которая гласит, что любая точка 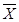 выпуклого замкнутого ограниченного множества К может быть представлена в виде выпуклой линейной комбинации конечного числа крайних точек этого множества,
выпуклого замкнутого ограниченного множества К может быть представлена в виде выпуклой линейной комбинации конечного числа крайних точек этого множества,
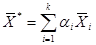 ,
, 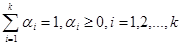 , (3.37)
, (3.37)
где 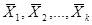 - крайние точки множества Р’.
- крайние точки множества Р’.
Выбросим из системы крайних точек 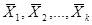 те, которые входят в разложение (3.37) с коэффициентом αi=0. Пусть это будут точки
те, которые входят в разложение (3.37) с коэффициентом αi=0. Пусть это будут точки
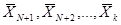 .
.
Тогда
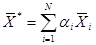 ,
,  ,
,
т.е. выполняются условия теоремы 1.5 и, следовательно,
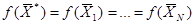 ,
,
что и доказывает теорему.
2. Пусть Р’ – неограниченное множество, а 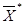 - конечное решение задачи линейного программирования.
- конечное решение задачи линейного программирования.
Тогда можно указать такое положительное число М, что
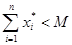 . (3.38)
. (3.38)
Введём в задачу линейного программирования дополнительное функциональное ограничение
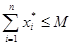 (3.39)
(3.39)
и рассмотрим новую задачу линейного программирования
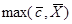 (3.40)
(3.40)
при условиях
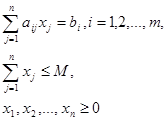 (3.40 – 3.42)
(3.40 – 3.42)
Множество планов данной задачи обозначим Р”. Множество Р” – ограниченное, а так как компоненты вектора 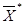 удовлетворяют условиям (3.40 – 3.42) и
удовлетворяют условиям (3.40 – 3.42) и 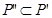 , то
, то 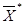 является решением задачи. Следовательно, согласно доказанному в случае 1 во множестве Р” существуют крайние точки
является решением задачи. Следовательно, согласно доказанному в случае 1 во множестве Р” существуют крайние точки 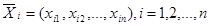 такие, что
такие, что
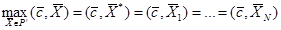
причём
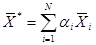 ,
, 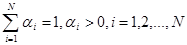 (3.43)
(3.43)
Если бы хотя бы одна крайняя точка 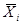 (i=1,2,…,N) не принадлежит гиперплоскости
(i=1,2,…,N) не принадлежит гиперплоскости 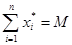 , (3.44)
, (3.44)
то она является крайней точкой множества Р’ и теорема доказана.
Пусть все крайние точки 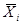 (i=1,2,…,N) принадлежат гиперплоскости (3.44), то есть имеют место равенства
(i=1,2,…,N) принадлежат гиперплоскости (3.44), то есть имеют место равенства
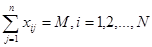
Тогда из (3.43) имеем 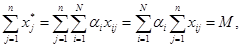
что противоречит условию (3.38) выбора М>0.
Теорема доказана.
7. Обоснование симплекс-метода решения КЗЛП: К-матрицы, условия перехода от одной К-матрицы к другой, изменение целевой функции при переходе от одной К-матрицы к другой, критерий оптимальности опорного плана, критерий неразрешимости ЗЛП (критерий неразрешимости без доказательства)
Пусть известна К-матрица
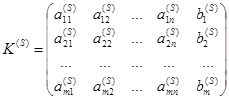 (3.45)
(3.45)
Обозначим через 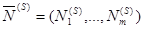 вектор номеров базисных (единичных) столбцов матрицы
вектор номеров базисных (единичных) столбцов матрицы  ,
, 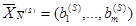 -вектор, компоненты которого есть базисные компоненты опорного плана, определяемого матрицей
-вектор, компоненты которого есть базисные компоненты опорного плана, определяемого матрицей  , и могут быть отличны от нуля. Остальные (n-m) компонент опорного плана, определяемого матрицей
, и могут быть отличны от нуля. Остальные (n-m) компонент опорного плана, определяемого матрицей  , равны нулю. Очевидно, что векторы
, равны нулю. Очевидно, что векторы 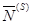 и
и 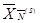 полностью задают опорный план, определяемый матрицей
полностью задают опорный план, определяемый матрицей  . Например, пусть
. Например, пусть
 =
= 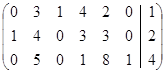 ,
,
тогда 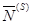 =(3,1,6);
=(3,1,6); 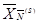 =
= 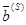 =(1,2,4) и, следовательно, опорный план, определяемый
=(1,2,4) и, следовательно, опорный план, определяемый  , имеет вид
, имеет вид
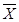 =(2,0,1,0,0,4).
=(2,0,1,0,0,4).
Итак, пусть К-матрица (3.45) определяет невырожденный опорный план
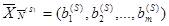
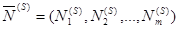 (3.46)
(3.46)
Выберем в матрице  столбец
столбец 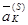 , не принадлежащий единичной подматрице, т.е.
, не принадлежащий единичной подматрице, т.е. 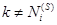 ,
, 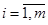 и такой, что в этом столбце есть хотя бы один элемент больше нуля.
и такой, что в этом столбце есть хотя бы один элемент больше нуля.
Пусть 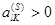 . Считая
. Считая 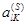 направляющим элементом, совершим над матрицей
направляющим элементом, совершим над матрицей  один шаг метода Жордана-Гаусса. В результате получим новую матрицу
один шаг метода Жордана-Гаусса. В результате получим новую матрицу
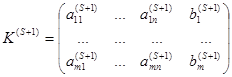 , (3.47)
, (3.47)
в которой столбец 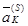 стал единичным, но которая может и не быть К-матрицей, так как среди величин
стал единичным, но которая может и не быть К-матрицей, так как среди величин 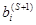 могут быть отрицательные. Условия выбора направляющего элемента
могут быть отрицательные. Условия выбора направляющего элемента 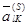 , позволяющие получить новую К-матрицу -
, позволяющие получить новую К-матрицу - 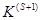 , т.е. обосновывающие способ перехода от опорного плана
, т.е. обосновывающие способ перехода от опорного плана 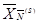 к опорному плану
к опорному плану 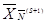 , составляет содержание следующей теоремы, которая была доказана выше.
, составляет содержание следующей теоремы, которая была доказана выше.
Теорема. (критерий оптимальности опорного плана) Пусть все симплекс-разности матрицы  неотрицательные. Тогда опорный план
неотрицательные. Тогда опорный план 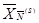 , определяемый матрицей
, определяемый матрицей  , является оптимальным.
, является оптимальным.
Доказательство.
По условию теоремы
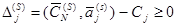
или
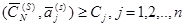 (3.52)
(3.52)
Пусть 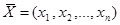 - произвольный план задачи линейного программирования. Умножим левую и правую части (3.52) на
- произвольный план задачи линейного программирования. Умножим левую и правую части (3.52) на 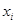 , тогда в силу неотрицательности
, тогда в силу неотрицательности 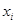 получим
получим
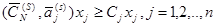 (3.53)
(3.53)
Согласно (3.53) имеем
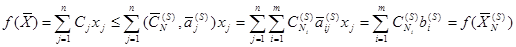
или
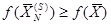 ,
,
что и доказывает теорему.
Теорема (критерий неразрешимости). Пусть в матрице  есть
есть 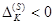 , и в столбце
, и в столбце 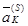 (
(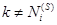 ,
, 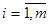 ) нет ни одного строго положительного элемента. Тогда ЗЛП (3.18) не имеет конечного решения.
) нет ни одного строго положительного элемента. Тогда ЗЛП (3.18) не имеет конечного решения.
8. Обоснование симплекс-метода решения КЗЛП: К-матрицы, условия перехода от одной К-матрицы к другой, изменение целевой функции при переходе от одной К-матрицы к другой, критерий оптимальности опорного плана (критерий оптимальности без доказательства), критерий неразрешимости ЗЛП.
Пусть известна К-матрица
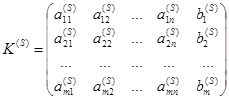 (3.45)
(3.45)
Обозначим через 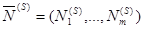 вектор номеров базисных (единичных) столбцов матрицы
вектор номеров базисных (единичных) столбцов матрицы  ,
, 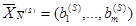 -вектор, компоненты которого есть базисные компоненты опорного плана, определяемого матрицей
-вектор, компоненты которого есть базисные компоненты опорного плана, определяемого матрицей  , и могут быть отличны от нуля. Остальные (n-m) компонент опорного плана, определяемого матрицей
, и могут быть отличны от нуля. Остальные (n-m) компонент опорного плана, определяемого матрицей  , равны нулю. Очевидно, что векторы
, равны нулю. Очевидно, что векторы 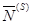 и
и 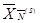 полностью задают опорный план, определяемый матрицей
полностью задают опорный план, определяемый матрицей  . Например, пусть
. Например, пусть
 =
= 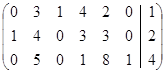 ,
,
тогда 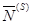 =(3,1,6);
=(3,1,6); 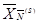 =
= 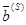 =(1,2,4) и, следовательно, опорный план, определяемый
=(1,2,4) и, следовательно, опорный план, определяемый  , имеет вид
, имеет вид
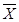 =(2,0,1,0,0,4).
=(2,0,1,0,0,4).
Итак, пусть К-матрица (3.45) определяет невырожденный опорный план
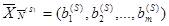
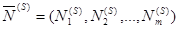 (3.46)
(3.46)
Выберем в матрице  столбец
столбец 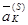 , не принадлежащий единичной подматрице, т.е.
, не принадлежащий единичной подматрице, т.е. 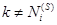 ,
, 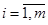 и такой, что в этом столбце есть хотя бы один элемент больше нуля.
и такой, что в этом столбце есть хотя бы один элемент больше нуля.
Пусть 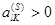 . Считая
. Считая 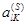 направляющим элементом, совершим над матрицей
направляющим элементом, совершим над матрицей  один шаг метода Жордана-Гаусса. В результате получим новую матрицу
один шаг метода Жордана-Гаусса. В результате получим новую матрицу
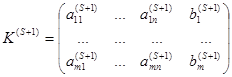 , (3.47)
, (3.47)
в которой столбец 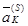 стал единичным, но которая может и не быть К-матрицей, так как среди величин
стал единичным, но которая может и не быть К-матрицей, так как среди величин 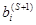 могут быть отрицательные. Условия выбора направляющего элемента
могут быть отрицательные. Условия выбора направляющего элемента 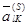 , позволяющие получить новую К-матрицу -
, позволяющие получить новую К-матрицу - 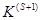 , т.е. обосновывающие способ перехода от опорного плана
, т.е. обосновывающие способ перехода от опорного плана 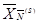 к опорному плану
к опорному плану 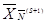 , составляет содержание следующей теоремы, которая была доказана выше.
, составляет содержание следующей теоремы, которая была доказана выше.
Теорема. (критерий оптимальности опорного плана) Пусть все симплекс-разности матрицы  неотрицательные. Тогда опорный план
неотрицательные. Тогда опорный план 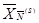 , определяемый матрицей
, определяемый матрицей  , является оптимальным.
, является оптимальным.
Теорема (критерий неразрешимости). Пусть в матрице  есть
есть 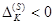 , и в столбце
, и в столбце 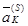 (
(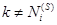 ,
, 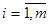 ) нет ни одного строго положительного элемента. Тогда ЗЛП (3.18) не имеет конечного решения.
) нет ни одного строго положительного элемента. Тогда ЗЛП (3.18) не имеет конечного решения.
Date: 2015-09-18; view: 563; Нарушение авторских прав