Исследование алгоритмов одномерной оптимизации

ЛАБОРАТОРНАЯ РАБОТА № 1

НАЗНАЧЕНИЕ И ЦЕЛЬ РАБОТЫ

Целью работы является изучение и анализ поисковых алгоритмов минимизации функции одной переменной: дихотомического, Фибоначчи и «золотого сечения».

ВВЕДЕНИЕ

В большинстве методов поисковой оптимизации, используемых в задачах параметрического синтеза конструкций и технологических процессов, таких как методы наискорейшего или покоординатного спуска, метод сопряженных направлений и т.п., на каждом шаге приходится решать задачу минимизации (максимизации) функции одной переменной. Действительно, после выбора в исходной точке 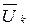( 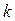-го шага) направления поиска 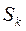, величина шага в этом направлении определяется из условия минимума (максимума) целевой функции 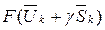, которая при фиксированных 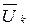и 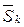является функцией одной скалярной переменной 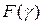. В результате решения этой задачи получают значение 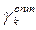и следующий шаг поиска начинают из точки .

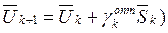Процедура нахождения 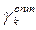представляет собой задачу поисковой одномерной оптимизации, различные методы одномерного поиска используют некоторый начальный интервал неопределенности 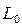, содержащий минимум (максимум) функции 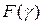, который затем уменьшается до некоторого значения 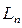путем вычисления значений функции в соответствующих точках и отбрасывания заведомо неоптимальных подынтервалов.

Будем для определенности рассматривать далее так называемые унимодальные функции 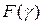, т.е. функции, имеющие на заданном интервале 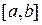единственный минимум. Не нарушая общности, будем полагать, что 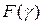минимизируется на интервале 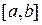; максимум функции находится подобным образом.

ДИХОТОМИЧЕСКИЙ МЕТОД

Этот метод предполагает на каждом шаге вычисление функции в двух точках (проведение двух экспериментов). При этом с целью максимального уменьшения интервала неопределенности на каждом шаге указанные точки выбираются как можно ближе к середине интервала.

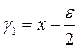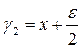Пусть на первом шаге эксперимент проводится в точках и , где 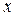– середина интервала 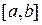, 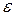– достаточно малое положительное число (это число модно трактовать как чувствительность экспериментатора в различении двух близких точек).

Рис.1

Если 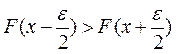, то с учетом унимодальности и возможности нахождения минимума в интервале 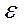для дальнейшего поиска должен быть оставлен интервал 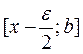, в противном случае – 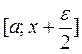. Таким образом, если вначале интервал неопределенности 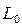равен 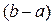, то после первого шага (состоящего из двух экспериментов) он равен

.

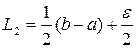Выберем теперь третий и четвертый эксперименты как 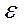пару в середине оставшегося интервала. После этого интервал неопределенности станет равным

.

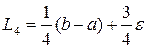Легко понять, что после 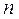экспериментов ( 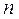– четно), произведенных по тому же правилу, минимум функции 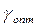лежит в интервале

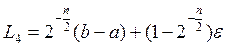. (1)

Из формулы (1) видно, что для уменьшения интервала неопределенности, например в 100 раз, если пренебречь величиной 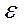, требуется 14 экспериментов.

Словесный алгоритм метода следующий:

Заданы начало 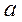и конец 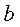интервала, точность .

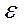Шаг 1. Рассчитывается середина интервала , .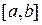

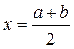Шаг 2. Рассчитываются точки 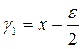и и 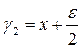значения в них целевой функци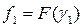и и .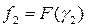

Шаг 3. Если 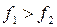, то 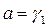, иначе .

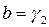Шаг 4. Повторять шаги 1-3 до тех пор, пока длина интервала 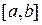больше .

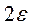Шаг 5. Результат .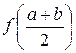

МЕТОД ФИБОНАЧЧИ

Этот метод является наиболее быстрым методом поиска, требующим минимального числа экспериментов. Здесь на каждом шаге, кроме первого, проводится не два, а один эксперимент. Стратегия поиска состоит в том, что новая точка поиска располагается внутри интервала неопределенности симметрично относительно уже находящейся там точки, оставшейся от предыдущих экспериментов. Для определения требуемого числа экспериментов 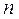, обеспечивающего точность, а также для выбора положения двух первых точек поиска, необходимо рассмотреть процесс поиска в обратном порядке, т.е. с последнего шага.

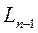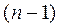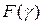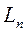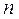Рассмотрим ситуацию, которая возникла после того, как все эксперименты, кроме последнего, уже проведены. Длину изменяющегося интервала неопределенности обозначим . Внутри этого интервала находится эксперимент с наименьшим из испытаний значением функции и внутри него также следует провести последний эксперимент. Очевидно, что для обеспечения минимального интервала неопределенности после экспериментов указанные точки должны быть симметрично расположены относительно середины интервала 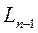и удалены от нее на расстояние .

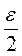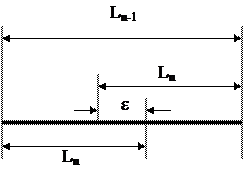
Рис. 2

Таким образом,

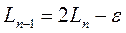. (2)

Рассмотрим далее ситуацию, когда проведены все эксперименты, кроме двух последних, и длину имеющегося интервала неопределенности обозначим 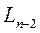. Внутри этого интервала находится точка с наименьшим из 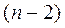испытаний значением 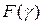, и также внутри него необходимо провести следующий 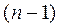эксперимент. По результатам этого эксперимента часть интервала 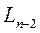должна быть отброшена, а оставшаяся часть есть 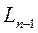. Поскольку заранее не ясно, какая часть будет отброшена, указанные точки должны располагаться на равных расстояниях от концов интервала .

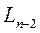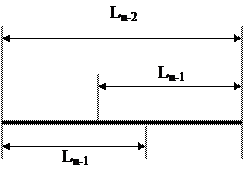
Рис.3

Но одна из точек внутри интервала 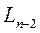останется после 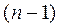эксперимента и станет точкой внутри интервала 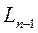. Сочетание возможных комбинаций рисунков 2 и 3 приводит к схеме разбиения интервала 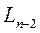, изображенных на рис. 4.

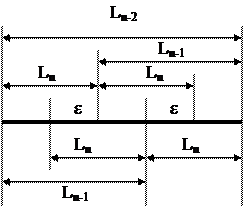
Рис.4

Из рис. 4 следует, что

.

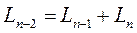Аналогично

.

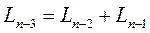В общем случае

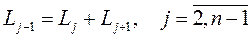. (3)

Таким образом,

,

,

,

.

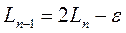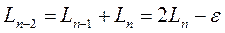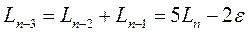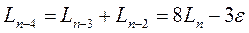Для получения общей формулы длины интервала 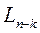введем последовательность чисел Фибоначчи 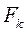, определяемую следующим образом:

,

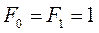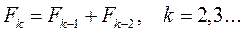(4)

Тогда имеем

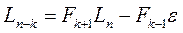(5)

Учитывая, что после первого испытания интервал неопределенности равен 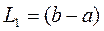, то полагая 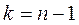, получаем:

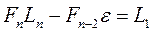
Отсюда

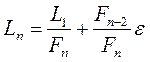(6)

Следовательно, после 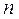экспериментов начальный интервал неопределенности, если пренебречь величиной 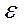, уменьшается в 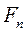раз. Для уменьшения интервала неопределенности, например в 100 раз, требуется 11 экспериментов.

Для того чтобы начать поиск по методу Фибоначчи, необходимо определить положение первых двух точек проведения испытаний. Эти точки располагаются симметрично внутри начального интервала неопределенности на расстоянии 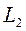от соответствующих концов этого интервала. Полагая в выражении (5) 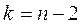, получаем

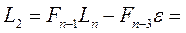
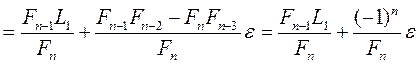
Пренебрегая величиной 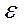, имеем

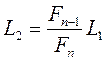. (7)

Словесный алгоритм метода следующий:

Заданы начало 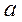и конец 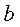интервала.

Шаг 1. Рассчитывается количество итераций 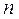и формируется массив чисел Фибоначчи.

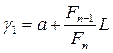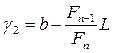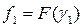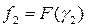Шаг 2. Рассчитываются две точки и и значения в них целевой функции и , где 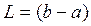– длина интервала .

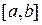Шаг 3. Если 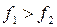, то

, , ,

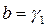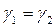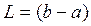
и рассчитывается одна новая точка

, ,

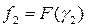иначе

, , ,

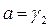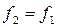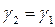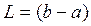
и рассчитывается одна новая точка

, .

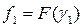Шаг 4. .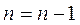

Шаг 5. Повторять шаги 1-3 до тех пор, пока .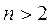

Шаг 6. Результат .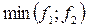

МЕТОД «ЗОЛОТОГО СЕЧЕНИЯ»

Для начала поиска по методу Фибоначчи необходимо предварительно задаться числом экспериментов 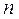исходя из допустимого значения интервала неопределенности в конце поиска. От этого недостатка свободен метод «золотого сечения», который почти столь же эффективен, как и метод Фибоначчи. Здесь так же, как и в последнем методе, точка, выбираемая внутри интервала неопределенности для проведения эксперимента на очередном шаге, располагается симметрично относительно уже находящейся там точки, оставшейся от предыдущих экспериментов. Поэтому здесь для трех соседних интервалов неопределенности также справедливо соотношение (3). Однако в методе «золотого сечения» не используется соотношение (2), которое зависит от 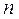. Вместо этого выдерживается постоянным, равным 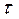, отношение длин последовательных интервалов, т.е.

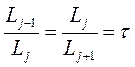. (8)

Разделив (3) на 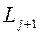и приняв во внимание, что согласно (8)

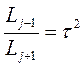, имеем 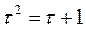, (9)

откуда

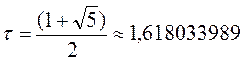. (10)

Тогда

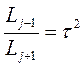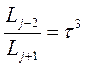; и т.д.

Следовательно,

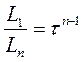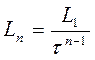, т.е (11)

Таким образом, в методе «золотого сечения» начальный отрезок делится по «правилу золотого сечения» (8), (10) и первые два эксперимента располагаются симметрично на расстоянии от соответствующих концов интервала. По результатам этих двух экспериментов сохраняется один из интервалов, в котором расположен оставшийся эксперимент. Симметрично ему располагается следующий эксперимент и т.д.

Можно показать, что окончательный интервал неопределенности в данном методе при достаточно больших 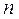всего лишь на 17% больше, чем в методе Фибоначчи. Можно показать также, что при больших 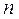оба метода начинаются практически из одной и той же точки.

Словесный алгоритм метода следующий:

Заданы начало 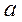и конец 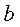интервала, точность , .

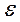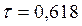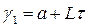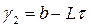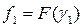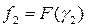Шаг 1. Рассчитываются две точки и и значения в них целевой функции и , где 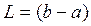– длина интервала .

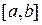Шаг 2. Если 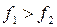, то

, , ,

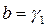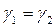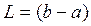
и рассчитывается одна новая точка

, ,

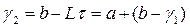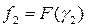иначе

, , ,

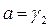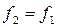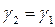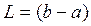
и рассчитывается одна новая точка

, .

.

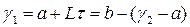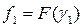Шаг 3. Повторять шаги 1-2 до тех пор, пока длина интервала 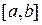больше .

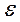Шаг 6. Результат .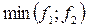

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Изучить теоретический материал.

2. Построить блок-схемы алгоритмов дихотомического деления, Фибоначчи, «золотого сечения».

3. Выбрать функцию по указанию преподавателя из таблицы и определить для нее начальный интервал поиска локального экстремума с помощью MathCAD.

4. Для алгоритма Фибоначчи определить количество экспериментов, позволяющее уменьшить интервал неопределенности в 1000 раз.

5. Осуществить по 2-3 итерации поиска экстремума заданной функции каждым из рассмотренных методов.

6. Разработать на ЭВМ программу, реализующую каждый из рассмотренных методов (язык программирования выбрать самостоятельно).

7. Получить решение задачи тремя методами с помощью разработанной программы.

СОДЕРЖАНИЕ ОТЧЕТА

1. Исходное задание на исследование.

2. Результаты, полученные в пп.3-5 порядка выполнения работы.

3. Блок-схемы алгоритмов.

4. Результаты машинного решения и их анализ.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Место задачи одномерного поиска в общей задаче оптимизации.

2. Сущность методов дихотомического деления, Фибоначчи, «золотого сечения».

3. Сравнительные характеристики исследуемых алгоритмов.

№	Функция	Экстремум
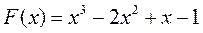
		минимум
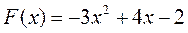
		максимум
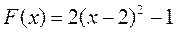
		минимум
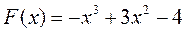
		максимум
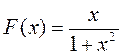
		минимум
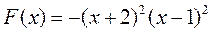
		максимум
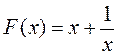
		минимум
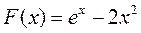
		максимум
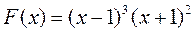
		минимум
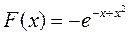
		максимум
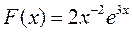
		минимум
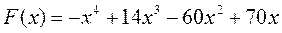
		максимум

Date: 2015-09-18; view: 629; Нарушение авторских прав