Идеальный цикл теплового двигателя Карно

Когда мы говорим об обратимости процессов, следует учитывать, что это некоторая идеализация. Все реальные процессы необратимы, поэтому и циклы, по которым работают тепловые машины, также необратимы, а значит и неравновесны. Однако для упрощения количественных оценок таких циклов необходимо считать их равновесными, то есть как если бы они состояли только из равновесных процессов. Этого требует хорошо разработанный аппарат классической термодинамики.

Знаменитый цикл идеального двигателя Карно считается равновесным обратным круговым процессом. В реальных условиях любой цикл не может быть идеальным, так как существуют потери. Он совершается между двумя источниками теплоты с постоянными температурами у теплоотдатчика Т₁ и теплоприемника Т ₂, а также рабочим телом, в качестве которого принят идеальный газ (рис. 3.1).

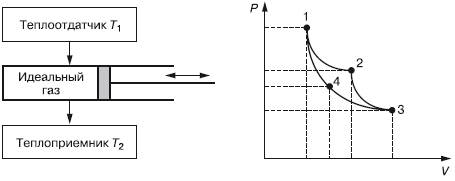
Рис. 3.1. Цикл теплового двигателя

Полагаем, что Т₁ > Т ₂ и отвод тепла от теплоотдатчика и подвод тепла к теплоприемнику не влияют на их температуры, T₁ и T₂ остаются постоянными. Обозначим параметры газа при левом крайнем положении поршня теплового двигателя: давление – Р₁ объем – V₁, температура Т ₁. Это точка 1 на графике на осях P-V. В этот момент газ (рабочее тело) взаимодействует с теплоотдатчиком, температура которого также Т ₁. При движении поршня вправо давление газа в цилиндре уменьшается, а объем увеличивается. Это будет продолжаться до прихода поршня в положение, определяемые точкой 2, где параметры рабочего тела (газа) примут значения P₂, V₂, T₂. Температура в этой точке остается неизменной, так как температура газа и теплоотдатчика одинакова в процессе перехода поршня от точки 1 к точке 2 (расширение). Такой процесс, при котором Т не изменяется, называется изотермическим, а кривая 1–2 называется изотермой. В этом процессе от теплоотдатчика к рабочему телу переходит теплота Q₁.

В точке 2 цилиндр полностью изолируется от внешней среды (теплообмена нет) и при дальнейшем движении поршня вправо уменьшение давления и увеличение объема происходит по кривой 2–3, которая называется адиабатой (процесс без теплообмена с внешней средой). Когда поршень переместится в крайнее правое положение (точка 3), процесс расширения закончится и параметры будут иметь значения Р₃, V₃, а температура станет равной температуре теплоприемника Т ₂. При этом положении поршня изоляция рабочего тела снижается и оно взаимодействует с теплоприемником. Если теперь увеличивать давление на поршень, то он будет перемещаться влево при неизменной температуре Т₂ (сжатие). Значит, этот процесс сжатия будет изотермическим. В этом процессе теплота Q₂ перейдет от рабочего тела к тепло-приемнику. Поршень, двигаясь влево, придет в точку 4 с параметрами P₄, V₄ и T₂, где рабочее тело вновь изолируется от внешней среды. Дальнейшее сжатие происходит по адиабате 4–1 с повышением температуры. В точке 1 сжатие заканчивается при параметрах рабочего тела P₁, V₁, T₁. Поршень возвратился в исходное состояние. В точке 1 изоляция рабочего тела от внешней среды снимается и цикл повторяется.

Таким образом, цикл Карно можно считать обратимым. Хотя при этом не учитывались различные сопутствующие потери (тепла в окружающую среду, на трение и некоторые другие условия идеализации).

Коэффициент полезного действия идеального двигателя Карно:

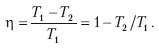
Анализ выражения для КПД цикла Карно позволяет сделать следующие выводы:

1) КПД тем больше, чем больше Т ₁ и чем меньше Т ₂;

2) КПД всегда меньше единицы;

3) КПД равен нулю при Т₁ = Т₂.

Цикл Карно дает наилучшие использования теплоты, но, как указывалось выше, он является идеализированным и в реальных условиях неосуществим. Однако значение его велико. Он позволяет определить наивысшее значение КПД теплового двигателя.

Date: 2015-09-18; view: 505; Нарушение авторских прав