
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Разработка и расчет эквивалентной динамической модели редуктора
|
|
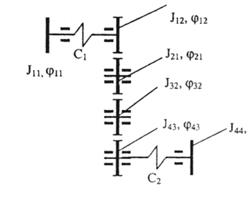
Рис.2. Эквивалентная динамическая модель редуктора
Определимся с обобщенными координатами
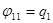 ;
;
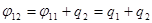 ;
;
 ;
;
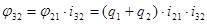 ;
;
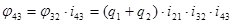 ;
;
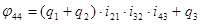 .
.
 Записываем выражения для кинетической и потенциальной энергий
Записываем выражения для кинетической и потенциальной энергий
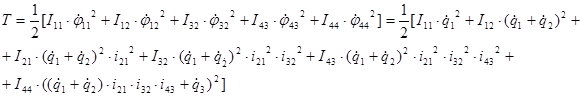
Раскроем скобки и возведем в квадрат члены в скобках
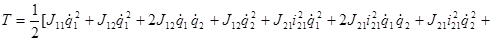
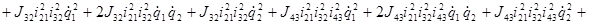
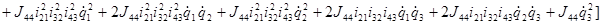
Объединим все подобные члены:
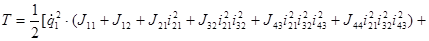
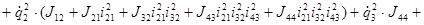
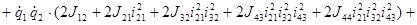
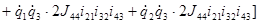 .
.
Окончательно выражение для кинетической энергии примет вид:
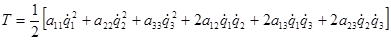 .
.
Введем обозначения:
 ;
;
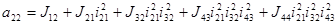 ;
;
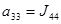 ;
;
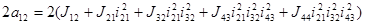 ;
;
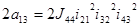 ;
;
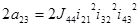 .
.
Где  ,
,  ,
, 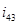 - передаточные отношения, равные:
- передаточные отношения, равные:
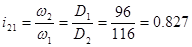 ;
;

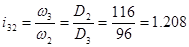 ;
;
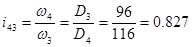 ;
;
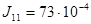 кг∙м2 – маховый момент электродвигателя;
кг∙м2 – маховый момент электродвигателя;
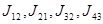 – суммы моментов инерции вала под шестерней и шестерни:
– суммы моментов инерции вала под шестерней и шестерни:
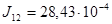 кг∙м2;
кг∙м2;
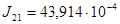 кг∙м2;
кг∙м2;
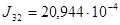 кг∙м2;
кг∙м2;
 кг∙м2;
кг∙м2;
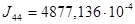 кг∙м2 – сумма моментов инерции вала под звёздочкой и звёздочки.
кг∙м2 – сумма моментов инерции вала под звёздочкой и звёздочки.
Подставив значения моментов и передаточных отношений, получим:
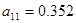 ;
; 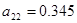 ;
; 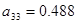 ;
; 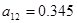 ;
;  ;
; 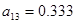 .
.
Запишем общее выражение для потенциальной энергии:

Запишем уравнение Лагранжа второго рода в обобщенных координатах:
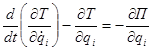 .
.
Тогда частные производные запишутся:
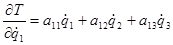 ;
;
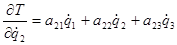 ;
;
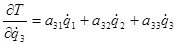 .
.
Взяв производные по времени, получим:
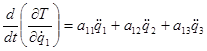 ;
;

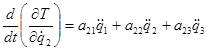 ;
;
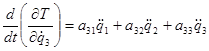 .
.
Из общего выражения потенциальной энергии, получим:
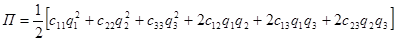 .
.
Найдем значение коэффициентов жесткости:
 ;
;
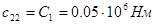
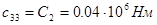
С учетом приведенных выше зависимостей запишем дифференциальные уравнения движения:
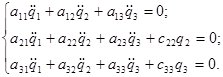 (
(
Обозначим:
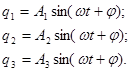
Подставив значения 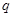 в систему и сократим на
в систему и сократим на 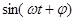
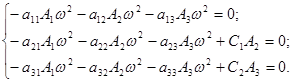
Из первых двух уравнений определим:
 ;
;
 .
.
Подставив оба выражения в третье уравнение и произведя преобразования, получим:


Обозначим и найдем коэффициенты биквадратного уравнения:
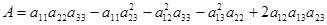 ;
;
 ;
;
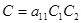 ;
;
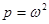 .
.
Получим: 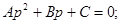
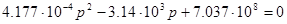 .
.
Решив биквадратное уравнение, найдем корни:
 ;
;  .
.
Откуда собственные частоты будут равны:
 ;
;
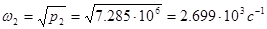 .
.
Date: 2015-09-03; view: 700; Нарушение авторских прав