Неадекватность ценовой формы

Цены по Хайеку создают систему связи для экономики. Но насколько адекватна эта связь и сколько информации она реально может передать? Пример Хайека о рынке олова подробно исследует этот вопрос. Следует сделать два предварительных замечания. Во-первых, рыночная система действительно добивается значительной степени координации экономических действий. «Анархия рынка» (Маркс) далека от полного хаоса. Во-вторых, даже в плановой системе всегда будет место для разочарованных ожиданий, для проектов, которые сначала выглядят многообещающими, а потом заканчиваются крахом, и так далее. И несмотря на все это, отлично видно, что Хайек чрезвычайно раздувает описанный им случай. Чтобы принять рациональные решения, как нужно изменить потребление олова, нужно знать, будет ли повышение цены постоянным или эпизодическим, а это требует знания, почему цены повысились. Сигнал со стороны цен сам по себе недостаточен. Подорожало ли олово временно из-за, скажем, забастовки шахтеров? Или мы приближаемся к истощению доступных запасов? Действия, рациональные в одном случае, будут совершенно неуместны в другом. По минимуму, можно сказать, что цены несут информацию о пропорции обмена различных товаров друг на друга в настоящий момент (если рынки находятся в равновесии, что бывает не всегда). Но отсюда не следует, что знание этих обменных пропорций позволяет агентам расчитать прибыльность, не говоря уже о социальной полезности, производства различных товаров. Произведенный товар может принести прибыль, если его цена выше суммы цен сырья, требующегося для его производства, и используется метод производства, при котором эта сумма наименьшая, но использование текущих цен в таких расчетах оправдано только в статическом контексте: или цены не меняются, или производство и продажа требуют нулевого времени. Хайек особо подчеркивает что перемены происходят постоянно, поэтому ему вряд ли понравилось бы это предположение. Будет ли производство товара х прибыльным на деле или нет, зависит не только от текущих, но и от будущих цен. А будет ли производство х считаться прибыльным в настоящий момент, зависит от текущих ожиданий будущих цен. Если мы начнем с предположения, что цены почти определенно не останутся в будущем стабильными, то как агенты могут строить свои ожидания? Одна возможность – они окажутся в состоянии собрать достаточно информации, чтобы сделать точный прогноз предполагаемых изменений. Но для этого им явно нужно знать намного больше, чем просто текущие цены. Они должны знать процесс, с помощью которого формируются цены, и создавать прогнозы развития различных факторов (хотя бы наиболее важных), влияющих на определение цен. Информационный минимализм Хайека тогда в значительной степени оказывается подорванным. Вторая возможность описана Кейнсом (Keynes, 1936, особенно гл. 12): агенты настолько ничего не знают о будущем, что хотя они и уверены, что некоторые (неизвестные) изменения произойдут, но прибегают к предположению, что завтрашние цены будут равны сегодняшним. Это позволяет им создать условную оценку прибыльности производства различных товаров, используя только текущую информацию о ценах; но издержки такого подхода (с точки зрения защитника эффективности рынка) – это доказательство внутренней, и возможно очень сильной, ошибочности таких предварительных оценок. В этом месте полезно обратиться к собственной теории Хайека о торговых циклах (Hayek, 1935; см. также Lawlor and Horn, 1992; Cottrell, 1994), в которой «дезинформация», переданная неравновесными ценами, может вызвать очень значительные макроэкономические искажения. В теории циклов Хайека ценой, вызывающей такой ущерб, становится процентная ставка, но ясно, что такой же точно аргумент можно применить и к микроуровню. Децентрализованные, ставящие целью максимизацию прибыли, реакции на нестабильные цены олова или микросхем памяти точно также могут вызвать ошибочные инвестиции и последующий хаос.

5.1. Цены, эффективность и «ноу-хау»

Одна из прогрессивных черт капитализма – процесс конкуренции в какой-то степени приводит к массовому переходу к методам производства, обладающим наименьшей себестоимостью (даже если эта себестоимость является денежными издержками производства, отражающими социальные издержки только частично и искаженно). Хайек совершенно верно напоминает нам, что такой переход может быть далеко не полным. Фирмы, производящие одни и те же товары (и возможно даже использующие одну и ту же базовую технологию) могут сосуществовать достаточно долгие периоды, несмотря на совершенно различную стоимость производства. Если закон одной цены относится ко всем рассматриваемым продуктам, то менее эффективные производители получат меньшую прибыль и/или будут платить более низкие зарплаты. Эта ситуация может долго продолжаться, если мобильность капитала и труда не идеальна. Встает вопрос: можно ли в плановой системе эффективнее стимулировать распространение лучшей практики? Мы считаем, что да. Если всем работникам будут платить за сделанную работу по унифицированной ставке, то неэффективные производители не смогут маскировать свою неэффективность, выплачивая низкие зарплаты. C использованием системы учета рабочего времени, которую мы обосновали в другом месте (Cockshott and Cottrell, 1989, 1993) разница в производственной эффективности будет сразу заметна. Помимо ее должны существовать и другие механизмы устранения разницы по мере их обнаружения. Частная фирма может заметить, что у конкурента себестоимость меньше, но кроме промышленного шпионажа у нее может и не найтись способа понять, за счет чего это достигнуто. Выравнивание эффективности, если оно вообще произойдет, может и не состояться, пока самый неэффективный производитель не разорится. С другой стороны, в рамках плановой системы некоторые управляющие или технические эксперты с более эффективных предприятий могут, например, могут быть отправлены в качестве экспертов на менее эффективные. Можно также представить себе - в отсутствие коммерческих секретов – электронные доски объявлений, где люди, занимающиеся определенными технологиями или производящие определенные товары, смогут обменяться советами и опытом по максимизации эффективности. Сегодняшняя популярность такого рода досок среди пользователей персональных компьютеров наводит на мысль, что их можно легко обобщить.

Информационные потоки при рынке и при плане

Один из наиболее фундаментальных аргументов Хайека состоит в том, что эффективное функционирование экономики предполагает использование большого количества распределенной информации, а задача централизации этой информации практически невозможна. В этом разделе мы подвергнем аргумент Хайека количественной проверке. Мы сравним издержки на связь, характерные для рыночных и для плановых систем, и изучим, насколько соответствующие издержки растут как функция масштаба экономики. Стоимость связи – это мера работы, которую нужно проделать, чтобы централизовать или распространить экономическую информацию: для измерения стоимости мы используем концептуальный аппарат алгоритмической теории информации (Chaitin, 1982). Существует большое количество литературы, изучающей такого рода вопросы в неоклассических терминах. Перед проведением нашего собственного анализа будут уместны некоторые комментарии, касающиеся стандартного подхода. В упомянутой литературе, обзор которой составил Жордан (Jordan, 1987), экономика характеризуется набором агентов, каждый из которых может послать одно или несколько сообщений. Получение этих сообщений другими агентами заставляет их изменить свои действия так, чтобы привести всю систему к равновесию. Предполагается, что эти сообщения – действительные переменные со знаком, а совокупное множество всех возможных сообщений, посылаемых всеми агентами, формирует евклидово векторное пространство. Информационные издержки системы считаются пропорциональными размерности векторов. Это определение очень абстрактно, и при попытке его конкретизации возникают проблемы. Во-первых, с точки зрения теории информации, считать сообщения действительными числами со знаком - значит приписывать им бесконечный объем информации. Если каждое сообщение требует бесконечной строки битов, то теряет смысл сравнивать издержки в терминах количества таких бесконечных строк, требующихся для выполнения задачи. Это, однако, относительно небольшая проблема, поскольку теоретическую работу такого типа можно почти определенно переформулировать в терминах сообщений, определенных на конечном подмножестве целых чисел. Более серьезная проблема относится к выбору размерности вектора сообщений как метрики стоимости информации. В работах Гурвича, Маунта, Рейтера и Жордана (главный вклад – Hurwicz, 1960), у каждого агента есть функция ответа, принимающая в качестве параметра вектор сообщений на текущем шаге, чтобы вычислить соответствующее действие для следующего шага. У Гурвича эти сообщения m определены как символы, взятые из определенного множества M. Непонятно, конечно ли это множество, но доказательство не изменится, если мы сделаем такое предположение, необходимое с точки зрения теории информации. Настоящая проблема заключается в том, что процесс, с помощью которого сообщения попадают от одного агента к другому, не рассмотрен. Собственно, предполагается, что сообщения передаются одновременно всем. Это неявное предположение крайне сомнительно. Широковещательная рассылка сообщений может быть выполнена только посредством дефицитного ресурса, например, части электромагнитного спектра. Если имеется радиостанция для рассылки таких сообщений, канал должен разделяться во времени между разными экономическими агентами: в один момент только один агент может послать сигнал и время, необходимое для одного цикла изменений, растет линейно с увеличением числа агентов. Но практически предположение, что сообщения имеют форму широковещательных радиосигналов, нереально, а если сообщения должны передаваться от каждого агента всем остальным в каждом цикле, то это можно сделать только путем размножения сообщений – почтой или чем-то подобным. В этом случае общее число посланных сообщений будет пропорционально квадрату числа агентов. В простом случае, когда каждый агент посылает в качестве сообщения целое число, количество посланных сообщений будет пропорционально квадрату размерности вектора сообщений. Таким образом, используя в качестве метрики размерность вектора сообщений, а не квадрат размерности, авторы серьезно недооценивают количество информации, которая должна быть передана в этой модели децентрализованной экономики. Если бы это была реалистическая модель, она могла бы только продемонстрировать невозможность работы любой большой конкурентной экономики из-за совершенно нелинейной функции информационных издержек, зависящей от числа агентов. Очевидно, что это относится к общему количеству писем, телексов или сообщений электронной почты, которые должны быть переданы. Кроме того, из модели вытекает, что агенты должны потратить для обработки входящей почты количество человеко-часов, пропорциональное числу агентов во всей экономике. Отсутствие реализма в таких моделях коренится в двух факторах: идее, что информация может быть каким-то образом доставлена всех участникам единственной операцией и в идее, что каждый агент должен обрабатывать сообщения от всех остальных. Мы попытались быть более реалистичными и более консервативными, оценивая информационные издержки рыночной экономики, поскольку мы явным образом подсчитываем все посланные индивидуальные сообщения и ограничиваем фирму приемом информации только от поставщиков и клиентов. При этих предположениях, которые намного благосклоннее к рыночной экономике, чем сделанные Жорданом, количество рассматриваемых нами сообщений является нижней границей их реального количества. В частности, мы явно опускаем все сообщения, связанные с оплатой и взаимозачетами чеков между банковскими счетами. Возвращаясь к главному ходу наших мыслей, наша стратегия - сначала рассмотреть динамическую проблему, насколько быстро и с какими затратами на связь экономика может придти к равновесию. Мы покажем, что плановая система может сделать это быстрее и с меньшей стоимостью связи. Сначала мы рассмотрим динамику изменений при статической цели, поскольку система управления с более быстрым ответом на воздействия будет также и быстрее отслеживать меняющуюся цель.

Рассмотрим экономику E = [ A, c, r, w] с n производителями, выпускающими различные товары при линейной зависимости результатов от затрат, использующими технологическую матрицу А с хорошо определенным вектором расходов на конечное потребление с, который не зависит от цен n товаров, извне заданным уровнем заработной платы w и сходной нормой прибыли r. Существует возможное равновесие по Сраффу e = [ U, p ], где U – матрица потока товаров и p – вектор цен. Мы предполагаем, как это делается при коммерческих расчетах, что все величины выражены с определенной конечной точностью, а не являются действительными числами. Сколько информации требуется, чтобы определить точку равновесия? Если у нас есть какой-то эффективный метод двоичного кодирования и I(s) есть мера битов информационного наполнения структуры данных s, использующей этот метод, тогда равновесие будет определено как I(e), или, поскольку равновесие в каком-то смысле задано стартовыми условиями, оно может быть указано как I(E) + I(p_s), где p_s – программа, для решения произвольной системы уравнений Сраффы. В общем случае I(e) ≤ I(E) + I(p_s). Мы предположим, что I(e) определяется через I(E) + I(p_s).

Пусть I(x|y) – условная или относительная информация (Chaitlin, 1982) об x при заданном y. Условная информация, связанная с любой произвольной конфигурацией экономики k = [ U_k, p_k ], тогда может быть выражена относительно точки равновесия e как I(k|e). Если k находится в окрестности e, то у нас I(k|e) ≤I(k). Например, предположим, что мы можем получить U_k из А и вектора интенсивности u_k, который указывает, с какой скоростью работает каждый завод. Тогда

,

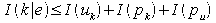где p_u – программа для вычисления U _k по каким-то А и u _k. Поскольку U _k – это матрица, а u _k – вектор, оба размерностью n, мы можем предположить, что I(U _k) > I(u _k).

Если экономика приближается к равновесию, условная информация, требующаяся для нахождения точки равновесия, уменьшается, поскольку u _k начинает приближаться к u _{e 7} . Интуитивно, мы должны только указать вектор отличий между этими двумя величинами, а для его кодирования будет требоваться все меньше и меньше информации по мере уменьшения расстояния между u _k и u _e. То же самое относится к двум векторам цен p _k и p _e. Если мы предположим, что система следует динамическому закону, заставляющему ее приближаться к равновесию, тогда имеем соотношение I(k_t+1|e) < I(k_t|e).

Теперь мы сконструируем модель количества информации, которая должна быть передана между производителями в рыночной экономике, чтобы продвинуть ее к равновесию, при следующих упрощениях: все производственные процессы требуют для работы одного шага времени, а вся экономика развивается синхронно. Мы предполагаем, что процесс начинается сразу после окончания производства, когда экономика находится в каком-то случайном неравновесном состоянии. Каждая фирма i выполняет следующий алгоритм:

1. Пишет всем своим поставщикам и спрашивает их текущие цены.

2. Отвечает на все запросы о ценах, указывая свою текущую цену p _i.

3. Открывает и читает все уведомления о ценах от своих поставщиков.

4. Оценивает текущую себестоимость единицы продукции.

5. Высчитывает ожидаемую прибыльность производства.

6. Если она ниже r, увеличивает (уменьшает) предполагаемый объем производства u _i на какую-то величину.

7. Рассчитывает, сколько единиц каждого сырья j нужно для поддержания такого объема.

8. Посылает каждому своему поставщику заказ на количество U _ij их товара.

9. Открывает все полученные заказы и

а) подсчитывает их общую величину;

б) если их общая величина больше, чем возможно выпустить товаров, пропорционально сокращает каждый заказ, чтобы товар был честно распределен между заказчиками;

в) отсылает подтверждение заказов своим клиентам (возможно, не на весь объем);

г) если у нее не осталось складских запасов, увеличивает продажную цену, пропорционально уровню избыточных заказов; если запасы остались, уменьшает цену пропорционально оставшимся запасам.

10. Получает все запрошенные комплектующие и сырье и определяет действительный размер производства.

11. Начинает производство для следующего периода.

Компьютерное моделирование систем такого рода показывает, что если готовность производителей менять цены слишком велика, то система может стать крайне нестабильной. Мы предполагаем, что изменения цен достаточно малы, поэтому происходят только затухающие колебания. Условие движения к равновесию тогда становится следующим: среди достаточно большого количества групп точек k фазового пространства средний эффект итерации вышеописанной процедуры заключается в уменьшении средней ошибки для каждой экономической переменной на какой-то множитель 0 ≤ g ≤ 1. В этом случае время выравнивания в векторном пространстве будет четко следовать логарифмическому закону – приведение ко множителю D в векторном пространстве займет время порядка log_1/8(D), а пространство времени выравнивания будет линейным. Таким образом, если во время t расстояние от равновесия равно I(k_t|e), выравнивание в пределах расстояния ε займет время порядка I(k_t|e):

,

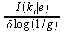где δ – константа, зависящая от числа экономических переменных, которые изменяются на каждом шаге на средний множитель g. Время выравнивания в экономическом пространстве для малых ε будет таким образом приближаться к линейной функции I(k|e), которую мы можем записать как Δ I(k | e). Теперь мы готовы выразить затраты на связь, необходимые для снижения условной энтропии экономики до какого-то уровня. Связь происходит на шагах 1, 2, 8 и 9в алгоритма. Сколько сообщений должен послать поставщик и сколько информации могут они содержать? Письма, посылаемые по почте, содержат много избыточной этикетной информации: мы предполагаем, что она устранена и сообщения сведены к их сути. Вся этикетная информация будет считаться единственным символом в ограниченном алфавите типов сообщений. Тогда запрос цены будет парой [R, H], где R – символ, показывающий, что сообщение является запросом цены и H – адрес запрашивающего. Ответ будет парой [Q,P], где Q указывает, что сообщение является предложением цены, а P – ценой. Аналогично заказ будет представлен как [O, U _ij], а с каждой поставкой будет отправляться уведомление [N, U_ij], где указывается реально отгруженное количество, причем U_ij ≤ U _ij. Если мы предположим, что каждая из n фирм имеет в среднем m поставщиков, количество сообщений каждого типа в одной итерации алгоритма будет равно nm. Поскольку мы имеем алфавит типов сообщений (R, Q, O, N) мощностью 4, эти символы могут быть закодированы 2 битами каждый. Мы также дополнительно предположим, что каждое сообщение (H, P, U _ij, U_ij) может быть закодировано двоичным числом, состоящим из b битов. Таким образом, мы получим выражение для затрат на связь для каждой итерации: 4nm(b+2). Учитывая число итераций, стоимость приближения к равновесию будет равна 4nm(b+2)I(k|e).

Теперь сравним, что потребуется в плановой экономике. В этом случае будет два раздельных алгоритма, один выполняет (государственная) фирма, другой – планирующий орган. Фирмы действуют следующим образом:

1. В первый период:

а) посылают плановикам сообщение, в котором указывают свой адрес, технические входные коэффициенты, текущие складские запасы;

б) получают от плановиков инструкции, какое количество каждого произведенного товара должно быть отослано каждой фирме;

в) посылают своим заказчикам товары с соответствующим уведомлением об отгрузке;

г) получают нужные для себя товары, читают уведомления об отгрузке и вычисляют новый объем производства;

д) начинают производство.

2. Затем они постоянно выполняют ту же последовательность действий, заменив шаг 1а следующим:

а) посылают плановикам сообщение, указывающее текущие складские запасы.

Планирующая организация выполняет следующий комплементарный алгоритм:

1. В первом периоде:

а) получает данные по складским запасам и техническим коэффициентам от всех фирм;

б) рассчитывает точку равновесия e по техническим коэффициентам и конечному спросу;

в) вычисляет магистраль развития (Dorfman, Samuelson ang Solow, 1958) от текущей структуры выходов до равновесной.

г) посылает фирмам указания, как согласовать их поставки с движением по магистрали.

2. Во втором и последующих периодах:

а) читает сообщения о степени выполнения плана;

б) вычисляет магистраль развития (Dorfman, Samuelson ang Solow, 1958) от текущей структуры выходов до равновесной.

в) посылает фирмам указания, как согласовать их поставки с движением по магистрали.

Мы предполагаем, что с помощью компьютерной технологии пункты б) и в) могут быть выполнены за относительно малое по сравнению с периодом производства время (Cockshott, 1990, Cockshot and Cottrell, 1993). При сравнении соответствующих информационных потоков становится ясно, что количество заказов и уведомлений, посылаемых на каждой итерации, одно и то же и при рынке, и при плане. Единственное различие – в случае плановой экономики заказы приходят из центра, а при рыночной – от заказчиков. Эти сообщения опять-таки требуют затрат на связь, равных 2nm(b+2). Разница в том, что в плановой системе нет обмена информацией о ценах. Вместо этого, на первом этапе передается информация о складских запасах и технических коэффициентах. Поскольку для передачи любого коэффициента требуется два числа, затраты на связь для фирмы будут (1+2m)b. Для n фирм эта величина приближается к nm(b+2), которые требуются для передачи данных о ценах. Разница возникает на следующих итерациях, когда при отсутствии технологических новшеств не нужно обновлять матрицу технологий, хранящуюся у плановиков. На i-1 следующих итерациях планирующая система должна обмениваться вполовину меньшим количеством информации, чем рыночная. Более того, поскольку плановая экономика движется по магистрали к точке равновесия, время выравнивания будет меньше, чем в рыночной экономике. Следовательно, издержки на связь будут равны 2nm(b+2)(2+(i-1)), где i < ΔI(k|e).

Следовательно, вопреки утверждению Хайека, количество информации, которая должна быть передана в плановой системе, значительно ниже, чем в рыночной. Централизованный сбор информации менее затруднителен, чем обмен коммерческой корреспонденцией, требуемый рынком. Кроме того, для выравнивания рыночной системе требуется больше времени. Влияние более быстрого выравнивания с целью адаптации к переменам в противовес стабильным условиям производства и потребления очевидно.

Date: 2015-09-03; view: 292; Нарушение авторских прав