Координатный способ задания движения точки. В выбранной системе координат задаются координаты движущейся точки как функции от времени

В выбранной системе координат задаются координаты движущейся точки как функции от времени. В прямоугольной декартовой системе координат это будут уравнения:

x =x(t)

y=y(t) (1.4)

z=z(t)

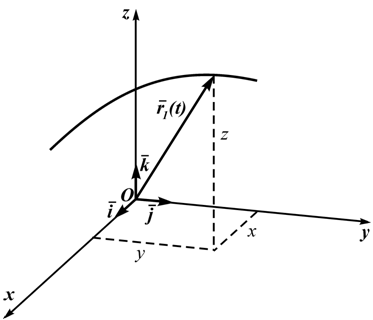
Рисунок 1.3

Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.

Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):

r(t)=i⋅x(t) ⊕ j⋅y(t) ⊕ k⋅z(t) (1.5)

Поэтому, используя формулы для определения скорости и ускорения точки при векторном способе задания движения, можно получить аналогичные формулы для координатного способа:

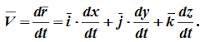
То есть:

Направление вектора скорости определяется с помощью направляющих косинусов:

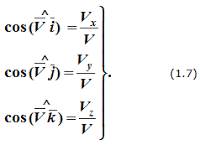
Формулы (1.6) и (1.7) полностью определяют вектор скорости при координатном способе задания движения точки, т.е. по величине и направлению.

5. Аналогичны формулы для определения ускорения точки:

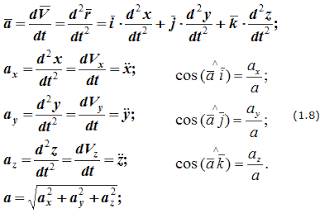
Формулы (1.8) определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.

.

6. Используется тогда, когда заранее известна траектория точки. Траекторию в этом случае считают криволинейной осью. На этой оси (как и на любой координатной) выделяют начало отсчета и положительное направление отсчета.

Положение точки на траектории определяется ее дуговой координатой s.

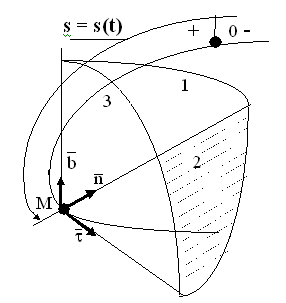Зависимость дуговой координаты от времени,

которая в общем виде записывается в виде s = s(t),

Date: 2015-09-03; view: 404; Нарушение авторских прав