Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Кинематика. 1.к инематикой называется раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения
|
|
1.к инематикой называется раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами и массами, определяющим это движение.
Система отсчета - это система координат жестко связанная с телом по отношению к которому изучается движение. Отсчет времени ведется с некоторого начального момента (t = 0).
Кинематически задать движение или закон движения - это задать положение движущегося тела относительно системы отсчета в любой момент времени.
Основная задача кинематики состоит в том, чтобы зная закон движения данного тела определить все кинематические характеристики как самого тела, так и его точек (траекторию, скорости, ускорения и т.д.).
Традиционно изучение кинематики начинают с точки.
Траекторией называют линию, которую описывает движущаяся точка в пространстве (рис. 15). Траектории весьма разнообразны: они могут иметь вид прямой линии, окружности, эллипса, параболы (I), циклоиды (II) и других кривых. Длина траектории при движении материальной точки характеризует пройденный путь. При движении по прямой от одной точки пространства к другой пройденный путь равен расстоянию между точками, при движении по другим траекториям путь получается больше расстояния.
Величина пути и продолжительность движения во времени определяют скорость движения.
Скорость есть быстрота перемещения тел от одной точки пространства к другой, которая определяется величиной пути, проходимого за единицу времени.
Движение тела с постоянной скоростью называют равномерным, движение с переменной скоростью — переменным.
Величина, определяющая изменение скорости с течением времени, называется ускорением.
Способы задания движения точки
Как уже отмечалось, чтобы задать движение точки, нужно задать ее положение в выбранной системе отсчета в любой момент времени. Существуют три способа задания движения: 1) естественный, 2) координатный, 3) векторный.
1) Естественный способ задания движения.
Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. В зависимости от вида траектории движение называют прямолинейным или криволинейным.
Пусть 
- система отсчета; АВ - траектория; О - начало отсчета; 
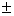- направление движения; S - криволинейная координата или расстояние вдоль дуги с соответствующим знаком (рис. 41 
).
Так как точка М движется вдоль траектории, то ее координата S будет изменяться со временем, то есть
S = f(t) (8.2.1)
Это и есть закон движения точки М вдоль траектории. Таким образом, чтобы задать движение точки естественным способом, надо задать: 1) траекторию точки. 2) начало отсчета на траектории с указанием направления движения (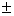), 3) закон движения точки вдоль траектории в виде (8.2.1).
Здесь необходимо заметить, что S определяет положение точки на траектории, а не пройденный путь.
2) Координатный способ задания движения.
Положение точки по отношению к данной системе отсчета O,x,y,z можно определить с помощью координат x,y,z (рис. 42 ). При движении точки М вдоль траектории, с течением времени, координаты будут изменяться и чтобы задать закон движения точки, нужно задать зависимости:
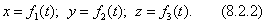
Соотношения (8.2.2) представляют собой уравнения движения точки в декартовых прямоугольных координатах. Они представляют собой и параметрические уравнения траектории. Исключив параметр t, получим уравнение траектории через координаты.
3) Векторный способ задания движения.
Пусть задана система отсчета Oxyz (рис. 43 ).
Положение точки М в ней, в любой момент времени можно определить, задав вектор r из точки О в точку М. Такой вектор называется радиус-вектором точки М. С течением времени он изменяется, то есть
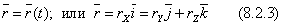
Это и есть закон движения точки в векторной форме. Годограф этого вектора определяет траекторию движения точки.
Определив все три закона движения, можно указать метод перехода от одного способа к другому.
Пусть уравнения движения заданы в форме (8.2.2), но
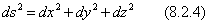
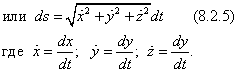
Задавая начальные условия: t = 0, S = 0 получаем
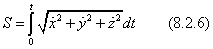
Это соотношение переводит закон движения из формы (8.2.2) в форму (8.2.1)
8.3.
Date: 2015-09-03; view: 402; Нарушение авторских прав