Скорость и ускорение точки при естественном способе задания движения

Пусть дана траектория и закон движения по ней (рис. 46 )

Это закон (8.2.1), S = f(t). Если за время 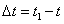точка переходит из положения М в положение 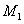, и криволинейная координата получает приращение 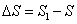, то численную величину средней скорости определяют как

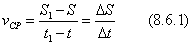
Переходя к пределу, получаем

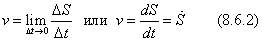
Численная величина скорости уточки в данный момент времени равна первой производной от координаты S по времени. Вектор скорости 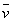направлен по касательной к траектории. Численная величина скорости v отличается от модуля скорости только знаком.

Численная величина одновременно определяет и модуль вектора скорости и сторону, куда он направлен.

Для определения ускорения при естественном способе задания движения, оси координат выберем следующим образом: ось 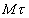- вдоль касательной к траектории, в сторону (+) направления отсчета расстояния S (рис. 47 ).

- ось Мn - по нормали, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости;

- ось Mb - перпендикулярно первым двум, так чтобы была правая тройка координатных векторов.

Нормаль Мn называется главной нормалью, а Мb - бинормалью.

Так как 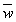лежит в соприкасающейся плоскости (см. 9.4), то есть в плоскости 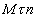, то его проекция на бинормаль равна нулю ().

Вычислим его проекции на две другие оси:

Пусть в момент времени t точка находится в положении М и имеет скорость 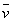, а в момент 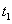- в положении 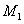со скоростью 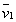. Тогда за промежуток 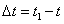она приобретет ускорение

Перейдем от векторов к их проекциям на оси 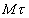и Мn, тогда

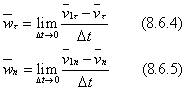
Проведем через точку 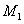оси 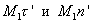, параллельные основным осям 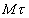и Мn. Обозначим угол между y, и осью 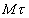через .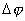

Этот угол между касательными к кривой в точках М и 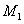назовем углом смежности, так как

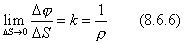
где 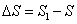, согласно рисунку 47.

Соотношение (8.6.6) определяет кривизну k кривой в точке М и определяется величиной, обратной радиусу кривизны 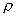. Учитывая (8.6.4), (8.6.5) и (8.6.6) запишем:

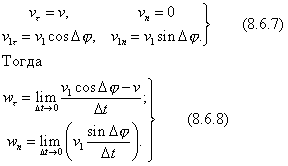
При 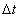стремящемся к нулю точка 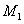будет находиться (стремиться) все ближе к точке М и 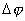, , будут так же стремиться к нулю, a 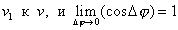, получаем для тангенциальной составляющей ускорения

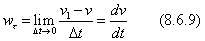
Для получения нормальной составляющей умножим и разделим второе соотношение (8.6.8) на :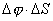

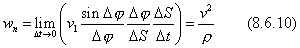
Результат 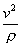получается в силу того, что

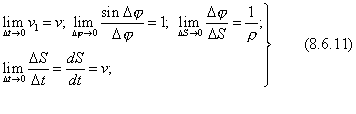
Окончательно получаем:

Проекция ускорения точки на касательную равна первой производной от численной величины скорости или второй производной от расстояния S по времени, а проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю.

Вектор ускорения точки 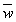всегда является диагональю параллелограмма, построенного на составляющих 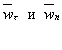(рис. 48 ).

Если касательная и нормальная составляющие полного ускорения записываются как (8.6.12), то

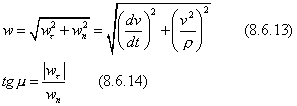
где 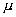- угол между вектором полного ускорения и нормалью к кривой в точке вычисления ускорения

7. Смысл такого представления ускорения (2.14) в том, что тангенциально (касательное)е ускорение а _t определяет изменение вектора скорости только по величине, а нормальная составляющая а_n связана с изменением вектора скорости только по направлению

Значение полного ускорения определяется как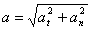

,

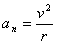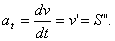
Date: 2015-09-03; view: 619; Нарушение авторских прав