Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Относительное, переносное и абсолютное движения. Лекция 4. Сложное движение точки и тела
|
|
Лекция 4. Сложное движение точки и тела
В данной лекции рассматриваются следующие вопросы:
1. Сложное движение точки.
2. Относительное, переносное и абсолютное движения.
3. Теорема сложения скоростей.
4. Теорема сложения ускорений. Ускорение Кориолиса.
5. Сложное движение твердого тела.
6. Цилиндрические зубчатые передачи.
7. Сложение поступательного и вращательного движений.
8. Винтовое движение.
Изучение данных вопросов необходимо в дальнейшем для динамики плоского движения твердого тела, динамики относительного движения материальной точки, для решения задач в дисциплинах «Теория машин и механизмов» и «Детали машин».
Сложное движение точки.
Относительное, переносное и абсолютное движения.
До сих пор мы изучали движение точки или тела по отношению к одной заданной системе отсчета. Однако в ряде случаев при решении задач механики оказывается целесообразным (а иногда и необходимым) рассматривать движение точки (или тела) одновременно по отношению к двум системам отсчета, из которых одна считается основной или условно неподвижной, а другая определенным образом движется по отношению к первой. Движение, совершаемое при этом точкой (или телом), называют составным или сложным. Например, шар, катящийся по палубе движущегося парохода, можно считать совершающим по отношению к берегу сложное движение, состоящее из качения по отношению к палубе (подвижная система отсчета), и движение вместе с палубой парохода по отношению к берегу (неподвижная система отсчета). Таким путем сложное движение шара разлагается на два более простых и более легко исследуемых.
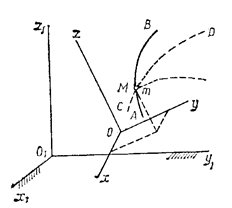
Рис.1
Рассмотрим точку М, движущуюся по отношению к подвижно системе отсчета Oxyz, которая в свою очередь как-то движется относительно другой системы отсчета O 1 x 1 y 1 z 1, которую называем основной или условно неподвижной (рис.1). Каждая из этих систем отсчета связана, конечно, с определенным телом, на чертеже не показанным. Введем следующие определения.
1. Движение, совершаемое точкой М по отношению к подвижной системе отсчета (к осям Oxyz), называется относительным движением (такое движение будет видеть наблюдатель, связанный с этими осями и перемещающийся вместе с ними). Траектория АВ, описываемая точкой в относительном движении, называется относительной траекторией. Скорость точки М по отношению к осям Oxyz называется относительной скоростью (обозначается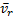 
), a ускорение - относительным ускорением (обозначается 
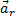). Из определения следует, что при вычислении 
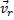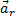и можно движение осей Oxyz во внимание не принимать (рассматривать их как неподвижные).
2. Движение, совершаемое подвижной системой отсчета Oxyz (и всеми неизменно связанными с нею точками пространства) по отношению к неподвижной системе O 1 x 1 y 1 z 1, является для точки М переносным движением.
Скорость той неизменно связанной с подвижными осями Oxyz точки m, с которой в данный момент времени совпадает движущаяся точка М, называется переносной скоростью точки М в этот момент (обозначается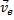 
), а ускорение этой точки m - переносным ускорением точки М (обозначается 
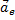). Таким образом,
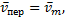
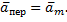
Если представить себе, что относительное движение точки происходит по поверхности (или внутри) твердого тела, с которым жестко связаны подвижные оси Oxyz, то переносной скоростью (или ускорением) точки М в данный момент времени будет скорость (или ускорение) той точки т тела, с которой в этот момент совпадает точка М.
3. Движение, совершаемое точкой по отношению к неподвижной системе отсчета O 1 x 1 y 1 z 1, называется абсолютным или сложным. Траектория CD этого движения называется абсолютной траекторией, скорость - абсолютной скоростью (обозначается 
) и ускорение - абсолютным ускорением (обозначается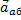 
).
В приведенном выше примере движение шара относительно палубы парохода будет относительным, а скорость - относительной скоростью шара; движение парохода по отношению к берегу будет для шара переносным движением, а скорость той точки палубы, которой в данный момент времени касается шар будет в этот момент его переносной скоростью; наконец, движение шара по отношению к берегу будет его абсолютным движением, а скорость - абсолютной скоростью шара.
При исследовании сложного движения точки полезно применять «Правило остановки». Для того, чтобы неподвижный наблюдатель увидел относительное движение точки, надо остановить переносное движение.
Тогда будет происходить только относительное движение. Относительное движение станет абсолютным. И наоборот, если остановить относительное движение, переносное станет абсолютным и неподвижный наблюдатель увидит только это переносное движение.
В последнем случае, при определении переносного движения точки, обнаруживается одно очень важное обстоятельство. Переносное движение точки зависит от того в какой момент будет остановлено относительное движение, от того, где точка находится на среде в этот момент. Так как, вообще говоря, все точки среды движутся по-разному. Поэтому логичнее определять переносное движение точки как абсолютное движение той точки среды, с которой совпадает в данный момент движущаяся точка.
Date: 2015-09-03; view: 542; Нарушение авторских прав