Некоторые частные случаи движения точки. Пользуясь полученными результатами, рассмотрим некоторые частные случаи движения точки

Пользуясь полученными результатами, рассмотрим некоторые частные случаи движения точки.

Равномерное прямолинейное движение

Равномерное прямолинейное движение - это движение, при котором тело за любые равные промежутки времени совершает равные перемещения, т. е. это движение с постоянной по модулю и направлению скоростью:

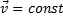— уравнение скорости,

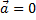— уравнение ускорения.

Пусть в момент времени t₀=0 координата тела х₀, в момент t - х (рис. 14).

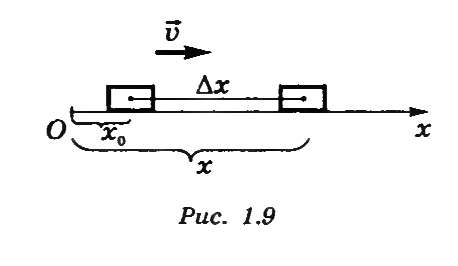
Рис.14

Тогда за промежуток времени Δt=t-t₀=t координата X тела изменилась на величину ∆х = х - х₀. Следовательно, проекция скорости тела

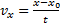,следовательно,

x=x₀+v_xt- кинематическое уравнение равномерного движения (уравнение зависимости координаты от времени).

Проекция перемещения ∆r_x=х-х₀

∆r_x=v_xt - уравнение перемещения.

При равномерном прямолинейном движении направление скорости не изменяется, поэтому путь 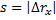. Следовательно, 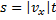— уравнение пути.

Зависимость кинематических величин от времени можно изобразить графически.

Изобразим графики скорости, перемещения, пути и координаты для трех тел: 1, 2, 3 (рис. 15).

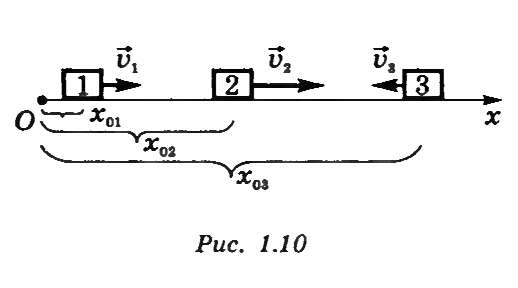
Рис.15

Тела 1, 2 движутся в положительном направлении оси Ох, причем ; тело 3 движется в направлении, про­тивоположном оси Ох; их начальные координаты соответственно 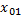, 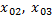. Графики скорости представлены на рис.16. Площадь заштрихованного прямоугольника численно равна пути s (модулю перемещения), пройденному телом 1 за время t₁. На рис.17 даны графики перемещения 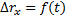, на рис.18 - графики пути s=f(t).

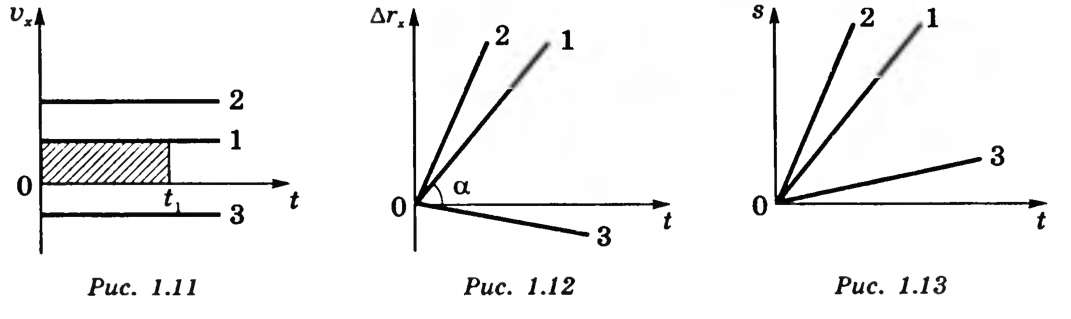
Рис.16 Рис.17 Рис.18

Наклон графика 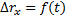, к оси времени зависит от модуля скорости: .

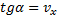Графики движения (зависимости координаты от времени) изображены на рис.19.

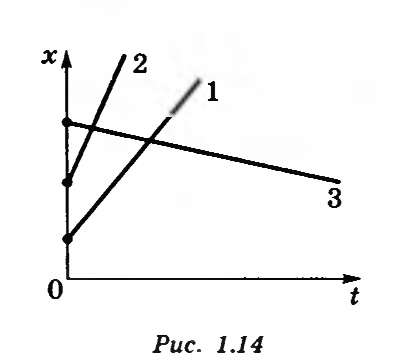
Рис.19

С помощью графика движения можно определить:

1) координаты тела в любой момент времени;

2) путь, пройденный телом за некоторый промежуток времени;

3) время, за которое пройден какой-то путь;

4) кратчайшее расстояние между телами в любой момент времени;

5) момент и место встречи тел и др.

Date: 2015-09-03; view: 505; Нарушение авторских прав