Определение ускорения при естественном способе задания движения. Касательное и нормальное ускорение точки

При естественном способе задания движения вектор 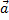определяют по его проекциям на оси Mτnb, имеющие начало в точке М и движущиеся вместе с нею (рис.11). Эти оси, называемые осями естественного трехгранника (или скоростными (естественными) осями), направлены следующим образом: ось Mτ - вдоль каса­тельной к траектории в сторону положительного отсчета расстояния s; ось Mn - по нормали, лежащей в соприкасающейся плос­кости и направленной в сторону вогнутости траектории; ось Mb - перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку. Нормаль Mn, лежащая в соприкасающейся плоскости(вплоскости самой кривой, если кривая плоская), называетсяглавной нормалью, а перпендикулярная к ней нормаль Mb - бинормалью.

Естественные оси – это подвижные оси, связанные с движущейся точкой М и образующие правую прямоугольную систему координат. Плоскость, проходящая через обе нормали (главную нормаль n и бинормаль b), называется нормальной плоскостью. Координатная плоскость, проходящая через касательную нормаль n, называется соприкасающейся плоскостью.

Соприкасающуюся плоскость в некоторой точке М кривой можно определить также, как предельное положение плоскости, прохо­дящей через касательную в точке М и любую точку кривой М₁, когда последняя стремится в пределе к совпадению с точкой М.

При движении точки по траектории направления естественных осей непрерывно изменяются.

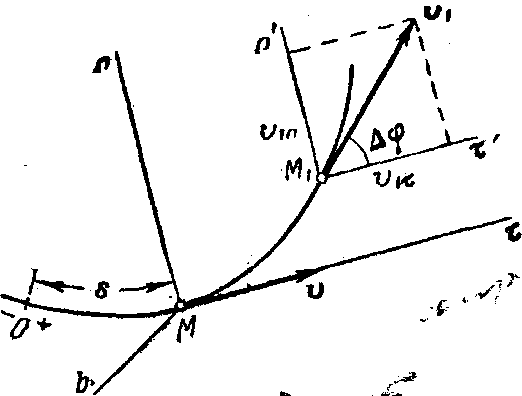
Рис.11

Было показано, что ускорение точки 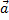лежит в соприкасающейся плоскости, т.е. в плоскости Mτn; следовательно, проекция вектора 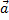на бинормаль равна нулю (a=0).

Вычислим проекции 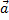, на две другие оси. Пусть в моментвремени t точка находится в положении М и имеет скорость v, a в момент t₁=t+∆t приходит в положение М ₁ и имеет скорость v₁.

Тогда по определению

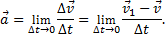
Перейдем в этом равенстве от векторов к их проекциям на оси Mτ и Mn, проведенные в точке М (рис.11). Тогда на основании теоремы о проекции суммы (или разности) векторов на ось получим:

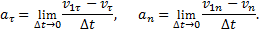
Учитывая, что проекция вектора на параллельные оси одинаковы, проведем через точку М ₁ оси 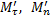, параллельные Mτ, Mn, и обозначим угол между направлением вектора 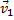и касательной Mτ через ∆φ. Этот угол между касательными к кривой в точках М и М ₁ называется углом смежности.

Напомним, что предел отношения угла смежности ∆φ к длине дуги MM₁=∆s определяет кривизну k кривой в точке М. Кривизна же является величиной, обратной радиусу кривизны ρ в точке М. Таким образом,

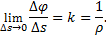
Обращаясь теперь к чертежу (рис.11), находим, что проекции векторов 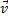и 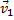на оси Mτ, Mn, будут равны:

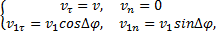
где v и v₁ - численные величины скорости точки в моменты t и t₁.

Следовательно,

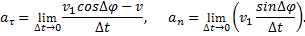
Заметим что при ∆t→0 точка М₁ неограниченно приближается к М и одновременно

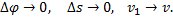
Тогда, учитывая, что в пределе , получим для a_τ выражение

Правую часть выражения a_n преобразуем так, чтобы в нее вошли отношения, пределы которых нам известны. Для этого умножим числитель и знаменатель дроби, стоящей под знаком предела, на ∆φ∆s. Тогда будем иметь

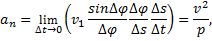
так как пределы каждого из стоящих в скобке сомножителей при ∆t→0 равны:

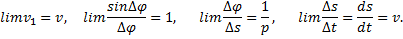
Окончательно получаем:

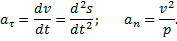
Итак, мы доказали, что проекция ускорения точки на каса­тельную равна первой производной от численной величины скорости или второй производной от расстояния (криволинейной координаты) s no времени, а проекция ускорения на главную нормаль равна квадрату скорости деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинор­маль равна нулю (a_b=0). Эти результаты выражают собою одну из важных теорем кинема­тики точки.

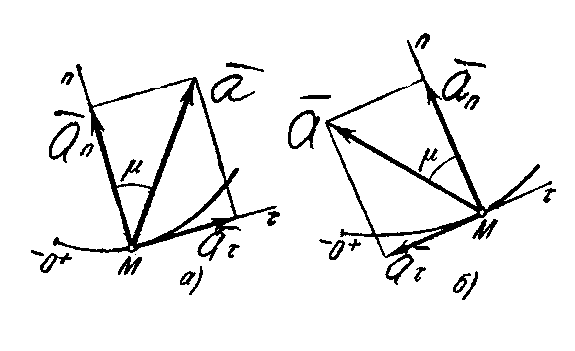
Рис.12

Отложим вдоль касатель­ной Mτ и главной нормали Mn векторы 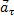и 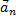, чис­ленно равные a_τ и a_n (рис. 12). Эти векторы изображают касательную и нормальную составляющие ускорения точки. При этом составляющая 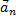бу­дет всегда направлена в сторону вогнутости кривой (величина a всегда положительна), а составляющая 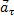может быть направлена или в положительном, или в отрицательном направлении оси Mτ в зависимости от знака проек­ции a_τ (см. рис.12, а и б).

Вектор ускорения точки 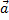изображается диагональю параллело­грамма, построенного на составляющих 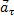и 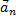. Так как эти состав­ляющие взаимно перпендикулярны, то по модулю:

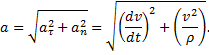
Date: 2015-09-03; view: 981; Нарушение авторских прав