Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Вектор скорости точки
|
|
Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий.
Скорость - мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.
Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с.
Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным.
Для равномерно-прямолинейного движения
∆r= v ∆t, (1)
где v – постоянный вектор.
Вектор v называется скоростью прямолинейного и равномерного движения полностью его определяет.
Из соотношения (1) видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени. Из (1) имеем
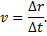
Направление вектора v указано на рис. 6.1.
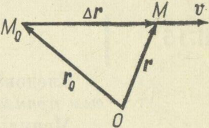
Рис.6.1
При неравномерном движении эта формула не годится. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени.
Пусть движущаяся точка находится в момент времени t в положении М, определяемом радиусом-вектором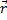 
, а в момент t1 приходит в положение M 1 определяемое вектором 
(рис.7). Тогда перемещение точки за промежуток времени ∆t=t1-t определяется вектором 
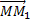который будем называть вектором перемещения точки. Из треугольника ОММ 1 видно, что 
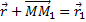; следовательно,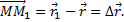 
Рис. 7
Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени ∆t:
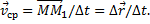
Скоростью точки в данный момент времени t называется векторная величина v, к которой стремится средняя скорость vср при стремлении промежутка времени ∆t к нулю:
Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени.
Так как предельным направлением секущей ММ 1 является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.
Date: 2015-09-03; view: 505; Нарушение авторских прав