
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные элементарные функции и наиболее важные функции
|
|
Используя известные сведения и приведенный алгоритм, можно сделать обзор графиков некоторых важных в приложениях функций.
Определение. Назовем основными элементарными функциями такие: степенная у=ха (а- действительное); показательная у=ах (а>0 и а  1); логарифмическая у=logax (а>0 и а
1); логарифмическая у=logax (а>0 и а  1); круговые тригонометрические y=Sinx, y=Cosx, y=tgx, y=ctgx; обратные тригонометрические y=arcSinx, y=arcCosx, y=arctgx, y=arcctgx. Они и служат базовыми при построении графиков других функций.
1); круговые тригонометрические y=Sinx, y=Cosx, y=tgx, y=ctgx; обратные тригонометрические y=arcSinx, y=arcCosx, y=arctgx, y=arcctgx. Они и служат базовыми при построении графиков других функций.
Опр. Все функции, которые получены из основных элементарных действиями сложения, вычитания, умножения, деления и наложения функциональной зависимости (суперпозиции), назовем элементарными.
Все остальные функции назовем неэлементарными.
Все степенные функции у=ха при а>0 имеют графики, которые условно можно назвать параболами. Схематическое их построение следует начинать с величины показателя а. Графики всех парабол проходят через две точки О(0;0) и А(1;1). При 0 < а < 1 ветви всех парабол изогнуты выпуклостью вверх, а при а >1 изогнуты выпуклостью вправо. После построения ветви параболы в
1-й четверти декартовой системы координат переходят к построению в других четвертях, используя свойство четности, нечетности и расположение области определения. Так, например, график функции y= 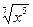 проходит через известные точки О и А, представлен выпуклой ветвью в 1-й четверти. Т.к. функция определена при любых х, то можно воспользоваться четностью и отразить центрально ветвь параболы из 1-й четверти в 3-ю (центр симметрии – начало координат точка О).
проходит через известные точки О и А, представлен выпуклой ветвью в 1-й четверти. Т.к. функция определена при любых х, то можно воспользоваться четностью и отразить центрально ветвь параболы из 1-й четверти в 3-ю (центр симметрии – начало координат точка О).
При отрицательном а графики степенных функций условно назовем гиперболами, т.к. схематически графики похожи на график обратно пропорциональной зависимости у= 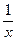 . Остальная схема построения графика изложена выше.
. Остальная схема построения графика изложена выше.
На основе графика функции у= 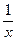 следует научиться строить график дробно-линейной функции у=
следует научиться строить график дробно-линейной функции у= 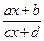 . Для этого сначала выполняют преобразование правой части равенства делением “уголком” и получают сумму целой части и правильной дроби. Затем приводят выражение к виду у=
. Для этого сначала выполняют преобразование правой части равенства делением “уголком” и получают сумму целой части и правильной дроби. Затем приводят выражение к виду у= 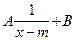 . Остается выполнить деформацию кривой у=
. Остается выполнить деформацию кривой у= 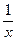 с коэффициентом А и затем реализовать сдвиг вдоль осей координат полученного графика.
с коэффициентом А и затем реализовать сдвиг вдоль осей координат полученного графика.
 |

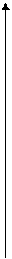 У у
У у
*(2;3)
 | |||
 | |||
* (1;1) + (0;1)
О х х
 |  | ||||
 |
+(-1;-1)
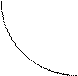
Рис 3.3. Базовая гипербола (слева) и преобразованная (справа)


 Приаер 3.3. Пусть нам требуется построить схематически график функции у=
Приаер 3.3. Пусть нам требуется построить схематически график функции у=  . Выполним деление “уголком” 2х-5 х-1 Получаем
. Выполним деление “уголком” 2х-5 х-1 Получаем
2х-2 2
 -3
-3
у= 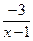 +2. Выполним растяжение графика с левого рисунка в 3 раза вдоль Оу
+2. Выполним растяжение графика с левого рисунка в 3 раза вдоль Оу
от Ох. Затем полученную кривую сдвинем вправо на 1 и вверх на 2. Получим правую кривую. При необходимости можно вычислить координаты точек пересечения результативной кривой с осями координат.
Показательную функцию у=ах (а>0 и а  1) часто называют экспонентой и обозначают так у=ехрах. Отметим, что все экспоненты проходят через точку (0;1). При 0 < а < 1 экспоненты убывают, но остаются положительными, а при
1) часто называют экспонентой и обозначают так у=ехрах. Отметим, что все экспоненты проходят через точку (0;1). При 0 < а < 1 экспоненты убывают, но остаются положительными, а при
а >1 все экспоненты возрастают, оставаясь положительными. Легко видеть, что при очень больших а и при очень малых а (но всегда положительных!) графики экспонент очень “крутые”. При а близких к 1 графики очень “пологие” и прижимаются к горизонтальной прямой у=1. Норвежский математик Непер предположил, что существует такое основание а, при котором касательная к экспоненте в точке (0;1) образует угол 45о с осью Ох. При дальнейших исследованиях выяснилось, что таким числов будет иррациональное число, значение которого приближенно равно 2,71828…. Это число принято называть числом Непера и обозначать буквой е. Т.о. имеем приближенное равенство
е= 2,71828…. Показательная функция с таким основанием записываеттся так у=ех или у=ехрх (символ онования функции подразумевается по умолчанию).
Графики экспонент приводить не будем в силу их общеизвестности.
Логарифмическая функция y=logax (а>0 и а  1) определяется (договор!) как обратная к экспоненте и потому подчиняется все свойствам обратной функции: область определения y=logax – положительные х (т.е. область значений экспоненты); график y=logax симметричен графику экспоненты относительно биссектрисы у=х первого и третьего координатных углов. Это значит, что все логарифмики (графики логарифмических функций) проходят через точку (1;0). При 0 < а < 1 все логарифмы – убывающие функции, а при
1) определяется (договор!) как обратная к экспоненте и потому подчиняется все свойствам обратной функции: область определения y=logax – положительные х (т.е. область значений экспоненты); график y=logax симметричен графику экспоненты относительно биссектрисы у=х первого и третьего координатных углов. Это значит, что все логарифмики (графики логарифмических функций) проходят через точку (1;0). При 0 < а < 1 все логарифмы – убывающие функции, а при
а >1 все логарифмы возрастающие функции. И при этом все графики расположены правее оси Оу. Наиболее широко используют логарифмы по основаниям 10 (обозначение y=lgx) и натуральные (неперовы) логарифмы (обозначение lnx). Последняя логарифмика обладает свойством – касательная к этой кривой в точке (1;0) проходит под углом 45о к оси Ох. Эта функция, наряду с функцией у=ех (или у=ехрх) наиболее применяемы в технических приложениях математики.
Круговые тригонометрические функции y=Sinx, y=Cosx,y=tgx, y=ctgx известны из школьного курса. Отметим лишь, что они периодические и потому обладают специфическими свойствами (см. 3.2.1). И что они поинтервально монотонны.
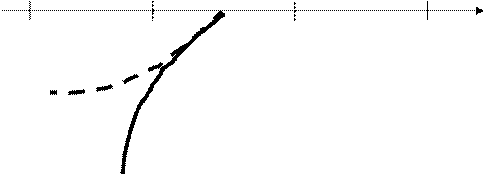
На основании круговых тригонометрических функций строятся обратные для них: y=arcSinx, y=arcCosx, y=arctgx, y=arcctgx. Графики обратных тригонометрических функций строят только для того участка области определения основной функции, на котором основная функция монотонна. Сначала строят монотонную часть основной функции. Затем полученный график отражают в биссектрисе 1-го и 3-го координатных углов. Ниже приведены рисунки построенных взаимно обратных функций y=Sinx и y=arcSinx, а также y=tgx и y=arctgx. Аналогично строятся графики функций
Y=arcCosx y=arcctgx.
 Y
Y

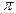 /2 y=arcSinx
/2 y=arcSinx


у=x
y=Sinx

 1
1 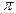
- 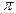 /2 -1 1
/2 -1 1 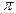 /2 X
/2 X
 |
 -1
-1
 -
- 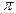 /2
/2


 Y
Y
 Y=tgx y=x
Y=tgx y=x

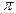 /2
/2

 y=arctgx
y=arctgx

 -
- 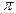 /2
/2 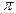 /2 X
/2 X
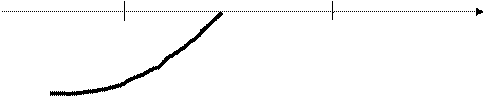 |
- 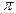 /2
/2

Рис 3.4. Примеры построения обратных функций
В математических приложениях применяются гиперболические функции. Рассмотрим только две из них y=Shx (гиперболический синус) и y=Chx (гиперболический косинус). Эти две функции определяются равенствами y=Shx= 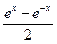 и y=Chx=
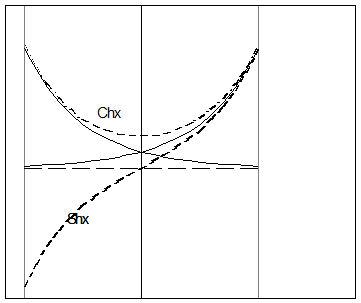
и y=Chx= 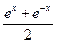 . В отличие от круговых тригонометрических функций (функций в круге), обладающих свойством Cos2x +Sin2x =1, гиперболические обладают свойством Cos2x - Sin2x =1. Первое из известных тождеств похоже на уравнение окружности с центром в начале координат и единичным радиусом (поэтому и функции в круге или круговые). А второе похоже на каноническое уравнение гиперболы (а потому и функции гиперболические). Графики этих функций строят схематически, используя принцип «суммирования ординат».
. В отличие от круговых тригонометрических функций (функций в круге), обладающих свойством Cos2x +Sin2x =1, гиперболические обладают свойством Cos2x - Sin2x =1. Первое из известных тождеств похоже на уравнение окружности с центром в начале координат и единичным радиусом (поэтому и функции в круге или круговые). А второе похоже на каноническое уравнение гиперболы (а потому и функции гиперболические). Графики этих функций строят схематически, используя принцип «суммирования ординат».
 |
 |
Рис 3.5. Построение Shx и Сhx суммированием экспонент 0,5е-х и 0,5ех
Известно, что линейная комбинация гармоник одинаковой частоты есть гармоника той же частоты. В самом деле
aSinkt+bCoskt= 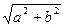 (
(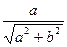 Sinkt+
Sinkt+ 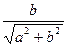 Coskt) =
Coskt) =
=A(CosфSinkt+Sinф Coskt)=Asin(kt+ф). В самом деле, выражения 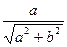 и
и 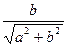 по модулю не превосходят 1, а в сумме дают 1. Поэтому они могут быть истолкованы как синус и косинус (в любом порядке; в данном случае они истолкованы так
по модулю не превосходят 1, а в сумме дают 1. Поэтому они могут быть истолкованы как синус и косинус (в любом порядке; в данном случае они истолкованы так 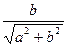 =Sinф
=Sinф 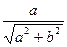 =Cosф). Далее применена формула синуса суммы двух углов (а может быть применена формула разности углов). Величина А, полученная в результате преобразования, носит название амплитуды гармоники k - частоты.
=Cosф). Далее применена формула синуса суммы двух углов (а может быть применена формула разности углов). Величина А, полученная в результате преобразования, носит название амплитуды гармоники k - частоты.
Руководствуясь такой схемой можно утверждать качественно, что графиком функции f(x)=elx Sin(kx+ф) будет график затухающиих (приl < 0) или развивающихся (приl > 0) колебаний, т.к. elx может быть истолкована как амплитуда этих колебаний.
Date: 2015-09-02; view: 911; Нарушение авторских прав